Der Spiegel
Christoph Pöppe
Das Gesicht, das Sie morgens über dem Waschtisch anschaut, das sind Sie selbst. Oder? Falsch. Wie jeder Ihrer Mitmenschen Ihnen bestätigen kann, sind Ihr Anblick im Original und im Spiegelbild ziemlich verschiedene Dinge. Jeder kennt Spiegel, und trotzdem sind sie irgendwie seltsam – was man seit dem 12. Februar in Heidelberg in der Ausstellung „Faszination Spiegelwelten“ bewundern kann.
Besonders ungewohnt wird es, wenn die verspiegelte Fläche krumm ist. Da schaut man auf die Spitze eines verspiegelten Kegels und findet eine ganz normale Szene vor. Auf dem Papier, auf dem der Kegel steht, findet sich jedoch eine merkwürdig kryptische Zeichnung. Erst auf den dritten Blick wird man gewahr, dass sie genau das Bild zeigt, das man über den Kegelspiegel sieht, nur eben grotesk verzerrt.

Ein Kleeblatt: Anamorphose mit Kegel in der MAINS Ausstellung „Faszination Spiegelwelten“
Ähnliches funktioniert, wenn der Spiegel die Form eines Zylinders statt eines Kegels hat. Die dafür gefertigten Zerrbilder heißen „Anamorphosen“ und haben eine lange Tradition in der bildenden Kunst.
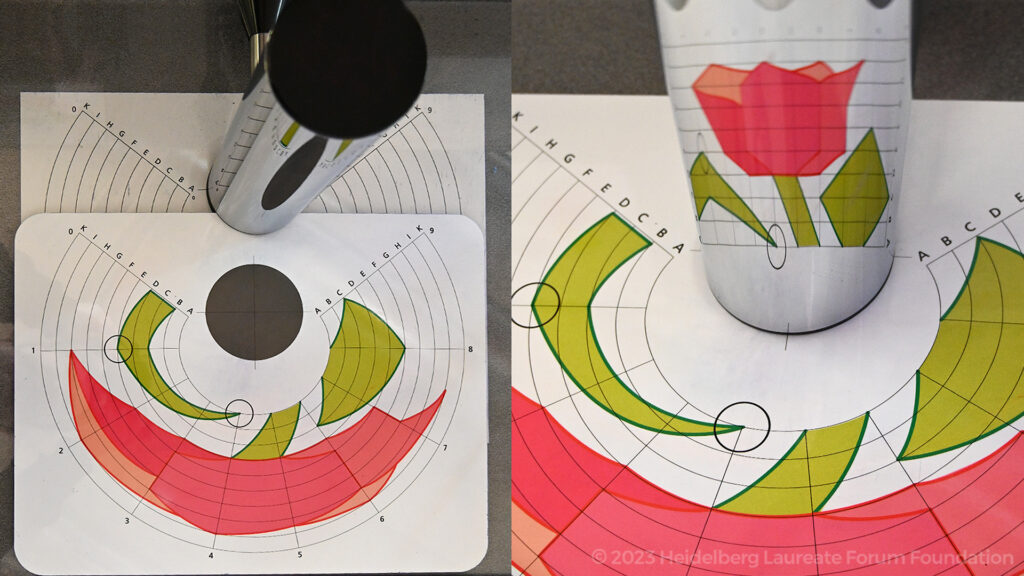
Eine Tulpe: Anamorphose mit Zylinder in der MAINS Ausstellung „Faszination Spiegelwelten“
Und wer vor einem Spiegel in Wellenform steht, sieht sich als dicker Gartenzwerg, als Bohnenstange oder als merkwürdige Mischung. Da stehen Ihnen die Haare zu Berge und vereinigen sich vielleicht sogar mit den Haaren Ihres kopfstehenden Doppelgängers.

Der „Zerr-/Wellenspiegel“ in der MAINS Ausstellung „Faszination Spiegelwelten“
Was die Lichtstrahlen alles anstellen auf dem Weg zum Spiegel und zurück, kann man natürlich auch nachrechnen. Das schlichte physikalische Gesetz „Einfallswinkel gleich Ausfallswinkel“ ist eigentlich alles, was man dazu braucht. Gemessen werden beide Winkel gegen die Senkrechte auf die Spiegelebene (das „Einfallslot“), und wo der Spiegel nicht eben ist, muss man in dem Punkt, wo der Lichtstrahl auftrifft, ersatzweise eine gedachte Ebene verwenden, die in diesem Punkt der krummen Fläche des Spiegels am nächsten kommt: die Tangentialebene. Ohne größeren Aufwand entdeckt man dann, dass ein Hohlspiegel dazu neigt, die eintreffenden Lichtstrahlen auf engem Raum zu konzentrieren, weswegen er in Scheinwerfern und Teleskopen Verwendung findet, während ein Konvexspiegel, also einer, der mir seinen dicken Bauch entgegenstreckt, das Licht eher zerstreut.
Und wenn die Spiegel alle eben sind? Dann gibt es keine Verzerrungen. Vielmehr sind Längen und Winkel im Spiegelbild genau so groß wie im Original. In der Sprache der Schulgeometrie: Original und Bild sind kongruent, die Spiegelung ist eine Kongruenzabbildung. Mit der kleinen Besonderheit, dass das Bild irgendwie „andersrum“ ist als das Original.
In diesem Zusammenhang kommt regelmäßig die Frage auf: „Warum vertauscht ein Spiegel rechts und links, aber nicht oben und unten?“ Die Antwort lautet: Er vertauscht gar nicht rechts und links. Vielmehr vertauscht er vorn und hinten. Nur: Wenn Sie vor dem Spiegel stehen, stellen Sie sich den Menschen, der Sie da anblickt, unwillkürlich so vor, als wäre Ihr zweites Ich hinter den Spiegel gewandert und hätte sich unterwegs um 180 Grad gedreht. Dieser gedachte Mensch trüge dann in der Tat den Ehering an der falschen Hand, er wäre Linkshänder, wenn Sie Rechtshänder sind, und wäre überhaupt in jeder Hinsicht seitenverkehrt. Das Spiegelbild einer rechtsdrehenden Spirale ist eine linksdrehende, und so weiter.
Wer gerne in Koordinaten denkt, kann sich den Spiegel in der (y, z)-Ebene eines dreidimensionalen Koordinatensystems vorstellen. Dann macht der Spiegel aus dem Punkt (x, y, z) den Punkt (–x, y, z). Und mit Mitteln der linearen Algebra kann man das noch etwas eleganter ausdrücken. Die Spiegelebene kann irgendwie schräg liegen, wenn nur der Nullpunkt in ihr liegt. Dann ist die Spiegelung an dieser Ebene eine lineare Abbildung mit Determinante –1. (Umgekehrt gilt das nicht! Lineare Abbildungen, selbst solche mit Determinante –1, können im Allgemeinen allerlei anstellen, was mit Spiegelung nicht mehr viel zu tun hat.)
Ein Gegenstand wird durch eine Spiegelung falschrum, und wenn dieses Spiegelbild nochmals gespiegelt wird, ist er wieder richtigrum. Die Regel „minus mal minus gibt plus“ gilt nämlich auch für Determinanten von Matrizen. Genauer: Zwei Spiegelungen an verschiedenen Ebenen sind dasselbe wie eine Drehung um die Gerade, die beiden Ebenen gemeinsam ist. Der Winkel der Drehung ist das Doppelte des Winkels, unter dem die Ebenen sich schneiden. Und bekanntlich ändert eine Drehung nichts an der Orientierung (richtigrum oder falschrum) des gedrehten Objekts.
Und wenn die Ebenen sich gar nicht schneiden, sondern parallel sind? Dann ist die doppelte Spiegelung nichts weiter als eine Parallelverschiebung, und zwar um zweimal den Vektor, der auf beiden Ebenen senkrecht steht und von der einen zur anderen weist. Das ist mit Matrizen allein zwar nicht mehr auszudrücken – schließlich können nicht beide Spiegelebenen zugleich durch den Nullpunkt gehen – aber die lineare Algebra stellt auch dafür die Mittel bereit.
Spiegelung, Drehung, Parallelverschiebung: Das ist bereits das vollständige Sortiment der Kongruenzabbildungen. Also kann man jede Abbildung, die Längen und Winkel unverändert lässt, aus Spiegelungen zusammensetzen. In der Tat haben manche Mathematiker die komplette Geometrie aus dem Spiegelungsbegriff aufgebaut. Damit rückt die Frage in den Mittelpunkt, was im Allgemeinen passiert, wenn man mehrere Spiegelungen hintereinander ausführt.
Wenn man ein und dieselbe Spiegelung zweimal hintereinander anwendet, landet man wieder beim Original. Wenn man sich das mit echten Spiegeln vorstellt, ist das einigermaßen absurd: Herr X steht davor und betrachtet sein Spiegelbild, nennen wir es Herrn Y. Den gibt es zwar nicht, aber wenn er dort hinter dem Spiegel stünde, wo Herr X ihn zu sehen glaubt, dann würde er im Spiegel (die Glasplatte ist von beiden Seiten verspiegelt) Herrn X sehen, und zwar genau dort, wo der real existierende Herr X steht.
Na gut; in der mathematischen Abstraktion ist das alles viel einfacher. Da ist das Spiegelbild so real wie das Original, denn beide gibt es nur in unserer Vorstellung. Und die mathematische Abbildung namens Spiegelung ist ihre eigene Umkehrung.
Nehmen wir jetzt an, wir haben zwei Spiegel und spiegeln erst am ersten, dann am zweiten, dann wieder am ersten und wieder am zweiten. Sind wir dann wieder zurück beim Original? Nein! Wenn die beiden Spiegel parallel sind, sind die ersten beiden Aktionen eine Parallelverschiebung und die letzten beiden dieselbe Parallelverschiebung noch einmal, und zweimal dieselbe Parallelverschiebung anwenden läuft nicht auf Nichtstun hinaus, sondern auf eine Parallelverschiebung mit dem doppelten Vektor. In der nächsten Runde Doppelspiegelung ist es der dreifache Vektor, dann der vierfache und so weiter.
Das können die Kinder in der Ausstellung in spektakulärer Weise erleben, indem sie in den innenverspiegelten „Unendlichkeitswürfel“ kriechen.

Der „Unendlichkeitswürfel“ in der MAINS Ausstellung „Faszination Spiegelwelten“
Und die Eltern können ihnen durch die Aussparungen oben dabei zuschauen.

Der „Unendlichkeitswürfel“ in der MAINS Ausstellung „Faszination Spiegelwelten“
Wiederholte Reflexion an Paaren paralleler Spiegel macht aus einem Kind ganz viele, verschoben mit dem einfachen, doppelten, dreifachen … Vektor. Und wenn nicht bei jeder Reflexion ein kleiner Teil des Lichts verlorenginge, könnte das Kind unendlich viele Bilder seiner selbst besichtigen, und das in allen drei Raumrichtungen und mit beiden Vorzeichen. Unsere beiden Spiegelungen, in umgekehrter Reihenfolge ausgeführt, ergeben eine Parallelverschiebung mit dem negativen Vektor.
Bei nicht-parallelen Spiegeln passiert etwas ganz Ähnliches. Die Vierfachspiegelung läuft auf zwei Drehungen mit demselben Winkel hinaus, also sind wir am Ende deutlich woanders als am Anfang. So wie oben die Verschiebungsvektoren addieren sich hier die Drehwinkel – wenn alle Drehungen um dieselbe Achse erfolgen.
Nur mit den unendlich vielen Spiegelbildern funktioniert das nicht so eindrucksvoll. Irgendwann wachsen die Drehwinkel über die 360 Grad hinaus, und dann mischen sich die neuen Bilder unter die alten, was ziemlich verwirrend aussieht, oder sie fallen mit den alten zusammen, wenn man sich geschickt anstellt, das heißt, einen Drehwinkel wählt, der gleich einem Teiler von 360 Grad ist.
Das kann man in der Ausstellung eigenhändig ausprobieren. Ein Ensemble von vier rautenförmig angeordneten Spiegeln ist mit einer Schnur verbunden, mit deren Hilfe man den Winkel zwischen zwei benachbarten Spiegeln variieren kann. Nur bei ganz bestimmten Stellungen fügen sich die Sternchen, die weiter innen angebracht sind, zu einem regelmäßig kreisförmigen Muster. In jeder anderen Stellung gibt es ein nicht sonderlich attraktives Durcheinander.
Der rautenförmige „Polytakis“ in der MAINS Ausstellung „Faszination Spiegelwelten“
Da die vier Spiegelebenen sich in lauter verschiedenen Geraden treffen, kommen auch Zusammensetzungen von Drehungen um verschiedene Achsen vor. Und da stellt sich heraus, dass es darauf ankommt, in welcher Reihenfolge zwei derartige Drehungen ausgeführt werden. Im Allgemeinen sind die Ergebnisse verschieden, und konkurrierende Vierfachspiegelbilder überlagern sich. Nur bei sehr speziellen Winkeln fallen die Bilder zusammen.
Wenn man jetzt noch ein bisschen weitersucht, nach einer Menge von Spiegelungen und Drehungen mit der Eigenschaft, dass die Zusammensetzung von zwei Abbildungen aus der Menge wieder zur Menge gehört, landet man ganz schnell bei der Gruppentheorie. (Eine Menge, die die genannte Bedingung und noch ein paar mehr erfüllt, nennt man eine Gruppe.) Und wenn alle Spiegelebenen durch den Nullpunkt gehen sollen und deswegen alle Drehungen, die sich aus diesen zusammensetzen lassen, den Nullpunkt unverändert lassen, und außerdem die gesamte Menge endlich sein soll: Dann gibt es gar nicht so viele Gruppen, die all diesen Forderungen genügen. Noch einen Schritt weiter, dann weiß man, warum es nur fünf platonische Körper gibt.
Na gut, das sieht man den Spiegeln nicht so unmittelbar an.
The post Der Spiegel originally appeared on the HLFF SciLogs blog.