Die seltsamen Fehlleistungen neuronaler Netze
Christoph Pöppe
Die Großtat, für die Adi Shamir berühmt wurde, ist schon eine ganze Weile her. Im Jahr 1977 erfand er, gerade mal 25 Jahre alt, gemeinsam mit Ron Rivest und Leonard Adleman das asymmetrische Kryptosystem, das nach den Anfangsbuchstaben seiner Erfinder RSA-Chiffre heißt und bis heute, wenn auch mit Modifikationen, beim Verschlüsseln von Nachrichten eine – jawohl – Schlüsselrolle spielt.
Aber Adi Shamir hat sich auf seinen frühen Meisterleistungen nicht ausgeruht. Auf dem diesjährigen Heidelberg Laureate Forum überrascht er sein Publikum mit Neuigkeiten aus einem Gebiet, das mit Kryptografie – bis auf die Zugehörigkeit zum großen Fach Informatik – nichts zu tun hat: neuronale Netze.
Das sind diese Schichten aus lauter einfachen Elementen, die Neuronen nachempfunden sind. Information fließt von den Neuronen einer Schicht zu denen der nächsthöheren Schicht, wird von diesen in relativ einfacher Weise verarbeitet und an die übernächste Schicht weitergereicht. Die Einzelheiten dieser Verarbeitung legt sich das Netz auf eine sehr spezielle Weise zu: durch Lernen an Beispielen. Neuronale Netze haben in den letzten Jahren sensationelle Erfolge erzielt, zum Beispiel den Weltmeister im Go-Spiel entthront. Sie stecken auch hinter den „large language models“ wie ChatGPT, die zumindest den Anschein eines Denk- oder gar Einfühlungsvermögens erwecken.
Angesichts dieser Erfolge ist es umso beunruhigender, dass neuronale Netze auf ihrem ursprünglichen Spielfeld, dem Erkennen von Bildern, unerklärliche Schwächen aufweisen. Ein Netz hat sehr viele Bilder von Katzen präsentiert bekommen und dabei gelernt, eine Katze zuverlässig von jedem anderen abgebildeten Gegenstand zu unterscheiden. Dann stört man ein Bild, das eindeutig eine Katze zeigt, mit einer minimalen Menge zufälliger Abweichungen, so klein, dass ein menschlicher Betrachter überhaupt keinen Unterschied sieht – und schon glaubt das Netz, das Bild zeige einen Weißstorch, eine Schüssel mit Guacamole oder was weiß ich.
Na ja – wenn ein solches neuronales Netz in einem autonomen Auto steckt und die Bilder seiner Kamera analysiert, legt man irgendwie schon Wert darauf, dass es nicht eine freie Strecke mit einer roten Ampel verwechselt oder umgekehrt. Entsprechend eifrig haben sich die Fachleute um eine Erklärung des Phänomens bemüht, bisher ohne nennenswerten Erfolg. An dieser Stelle bietet Adi Shamir gemeinsam mit Odelia Melamed und Oriel BenShmuel vom Weizmann Institute of Science in Rehovot (Israel) eine neue Idee an. Die entscheidenden Gedanken kommen dabei bemerkenswerterweise aus der Geometrie.
In ihrer Arbeit nehmen Shamir, Melamed und BenShmuel der Klarheit der Darstellung zuliebe einige heftige Vereinfachungen vor. So unterstellen sie, ihr neuronales Netz habe nur gelernt, zwischen zwei Sorten von Bildern zu unterscheiden: „Katze“ und „Pampe“ (im Original Guacamole). Und während echte neuronale Netze in ihrer untersten Schicht die Farbwerte der Pixel entgegennehmen, aus denen das Bild besteht, ist es in der Vereinfachung nur eine einzige reelle Zahl pro Pixel.
Ein ausgelerntes neuronales Netz tut dasselbe wie ein Computerprogramm, das zu einem x das f(x) berechnet: eine Funktion auswerten. Das x ist ein Bild und das f(x) eine reelle Zahl, die angibt, wie stark dieses Bild das Merkmal „Katze“ aufweist. Wie die Funktion f definiert ist und wie das Netz sie berechnet: Das wissen wir nicht so genau. Die Einzelheiten der Berechnung hat es ja nicht einprogrammiert bekommen, sondern gelernt: indem ein „Lehrer“ ihm viele Beispielbilder vorlegte und dazusagte, ob es sich um Katze oder Pampe handelt. Immerhin wissen wir, dass unsere Funktion bei jedem der gelernten Katzenbilder einen hohen positiven Wert annimmt und bei jedem Pampenbild einen sehr negativen.
In dem abstrakten Raum aller denkbaren Bilder – ja, jedes Bild ist genau ein Punkt in diesem Raum! – wandern wir jetzt in Gedanken von einem Punkt mit sehr positivem f-Wert (sprich Katzenbild) zu einem mit sehr negativem f-Wert (Pampenbild). Die Punkte unterwegs sind dann Bilder, die einen sehr allmählichen Übergang vom einen zum anderen Bild darstellen. Dann ist irgendwo auf dem Weg f(x) = 0. (Ja, f ist stetig, und es gilt der Zwischenwertsatz.) Das gilt für alle Wege von der einen zur anderen Bildersorte.
Wenn der Raum aller Bilder jetzt zweidimensional wäre, so dass wir ihn uns richtig leicht vorstellen könnten, dann gäbe es in diesem Raum Katzenbezirke und Pampenbezirke. Möglicherweise gibt es von jeder Sorte mehrere Bezirke, die nicht miteinander zusammenhängen. Auf jeden Fall sind die Bezirke säuberlich getrennt, und zwar durch eine Kurve: die Menge aller Punkte, auf denen f(x) = 0 ist.
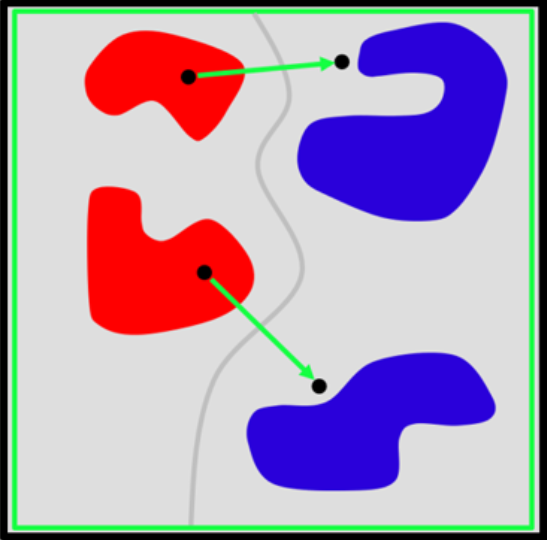
Leider hat der Raum aller Bilder nicht nur zwei Dimensionen, sondern so viele, wie ein Bild Pixel hat: Größenordnung eine Million. Die Funktion f gibt es immer noch, und deren Nullstellenmenge ebenfalls. In drei Dimensionen wäre es eine Fläche, und standardmäßig hat sie eine Dimension weniger als der Raum, in dem sie lebt. Die Fachleute sagen an dieser Stelle „Mannigfaltigkeit“ statt „Fläche“; denn zweidimensonal ist sie beim besten Willen nicht. Eine 999999-dimensionale Teilmenge eines millionendimensionalen Raums ist eine erhebliche Herausforderung für das Vorstellungsvermögen; aber man kann abstrakte Aussagen über sie machen.
Zum Beispiel kann die Trennfläche nicht beliebig verknittert sein. Denn sie ist das Ergebnis einer Berechnung durch – zugegeben: zahlreiche – Neuronen, die jedes für sich sehr einfach gebaut sind. Da können so exotische Dinge wie fraktale Verknitterungen gar nicht vorkommen. Und das oben genannte Verwechslungsproblem dürfte eigentlich auch nicht auftreten.
Unsere Funktion f ist stetig: erstens, weil die Neuronen konstruktionsbedingt nicht anders können, zweitens weil sich das beim Lernprozess ohnehin ergeben sollte. Das Netz soll ja ein Katzenbild mit geringen Abweichungen, also einen Punkt in unmittelbarer Nähe des Katzenbilds, noch als Katzenbild erkennen. Anders ausgedrückt: Die Funktion f soll von einem positiven Wert nicht plötzlich steil auf null und gar darunter abfallen. Genau das passiert aber.
Shamir und Kollegen bieten dafür folgende Erklärung an: Alle von einer Digitalkamera aufgenommenen und nicht raffiniert manipulierten Bilder sind in einem speziellen Sinne „ordentlich“. Sie enthalten eben nicht die zufälligen kleinen Abweichungen von der „richtigen“ Bildgestalt, die ein neuronales Netz so spektakulär in die Irre führen können. Insbesondere sind alle Bilder, Katze wie Pampe, an denen das Netz trainiert wird, ordentlich. In dem abstrakten Raum aller Bilder sind die ordentlichen eine sehr kleine und vor allem dünne Teilmenge. Je nachdem, wie man den Begriff „ordentlich“ definiert, was nicht einfach ist, liegt ihre Dimension um das Zehn- bis Hundertfache unter der des ganzen Raums.
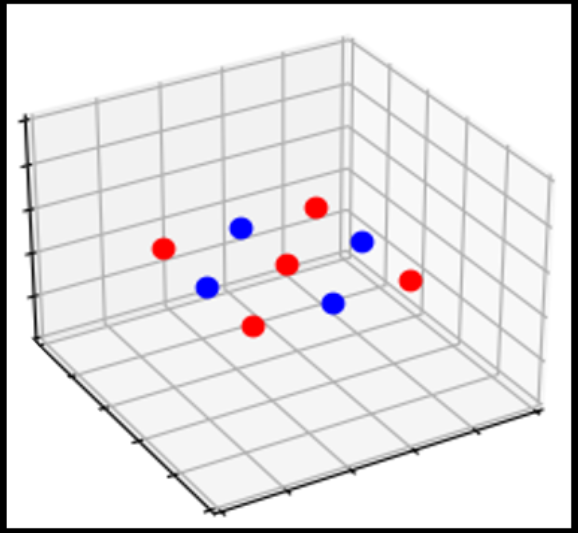
Wie dem auch sei: Im Verlauf des Lernprozesses merkt das Netz gewissermaßen sehr schnell, dass es überhaupt nur um ordentliche Bilder geht, und legt seine Trennfläche zwischen Katze und Pampe in einer ersten Phase so, dass sie im Wesentlichen der Teilmenge der ordentlichen Bilder folgt. Erst in der zweiten Phase kommt die Feinabstimmung: Wenn sich herausstellt, dass ein Katzenbild noch auf der falschen Seite der Trennfläche liegt, kommen die Zwerge mit kleinen Hämmerchen und schlagen eine Delle in die Trennfläche, bis die auf der richtigen Seite am Katzenbild vorbei verläuft. Dasselbe geschieht in umgekehrter Richtung, falls ein Pampenbild sich als fehlplatziert herausstellen sollte.
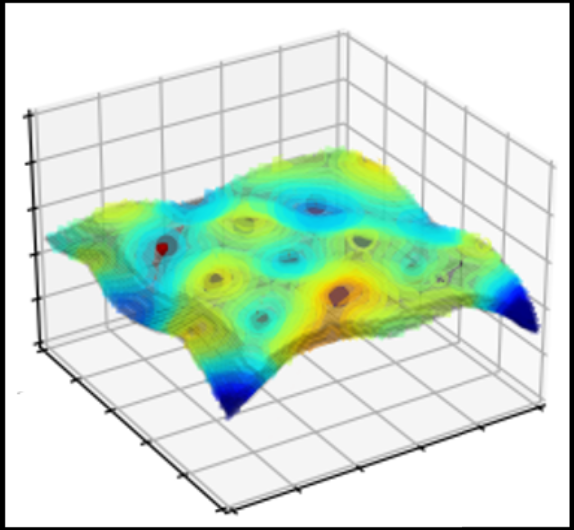
Was wollen uns die Autoren mit der seltsamen Metapher von den Zwergen und den Hämmerchen sagen? Mehrere Dinge. Erstens ist es eine gute Idee, sich die Trennfläche aus dünnem Blech vorzustellen. Klopft man es an einer Stelle zurecht, dann geht die unmittelbare Umgebung mit. Das ist eine andere Ausdrucksweise dafür, dass die Funktion f stetig und die Trennfläche nicht zu heftig gekrümmt sein sollte.
Zweitens: Wenn man auf das Blech klopft, beult es sich in einer Richtung aus, die senkrecht zur Ausbreitungsrichtung des Blechs ist. Jawohl, auch in hochdimensionalen Räumen kann man sinnvoll von rechten Winkeln reden. Allerdings gibt es hier sehr viele verschiedene Richtungen, die alle senkrecht auf dem Blech stehen. Da nun die Trennfläche im Wesentlichen der Menge der ordentlichen Bilder folgt, treibt jeder Hammerschlag sie von dieser Menge weg, in die wüsten Gefilde der unordentlichen Bilder. Einmal dort hingeraten, wird sie in der Tendenz dort bleiben. Denn da das Netz nie ein unordentliches Bild zu sehen bekommt, hat es auch keine Gelegenheit, die Position der Trennfläche im Reich des Unordentlichen zu korrigieren.
Drittens: Es sind sehr viele sehr kleine Hammerschläge. So ist das übliche Fehlerkorrekturverfahren („backpropagation“) gebaut. Das heißt, die Dellen im Blech sind ziemlich flach, gerade so tief, wie es sein muss, damit das Netz ein ordentliches Bild richtig erkennt. Das wiederum hat zur Folge, dass man von einem ordentlichen Bild nur ein kurzes Stück in die falsche Richtung wandern muss, um auf die Trennfläche zu treffen, und noch ein kleines Stück darüber hinaus, um auf die falsche Seite zu geraten.
So weit die stark vereinfacht dargestellte Idee. Wenn man die oben genannten Einschränkungen aufhebt – Farb- statt Schwarzweißwerte, mehr als zwei Klassen von Bildern –, wird die Sache unübersichtlicher, aber nicht prinzipiell schwieriger. Andere Einzelheiten, über die ich hinweggegangen bin, wollen ausgearbeitet werden, was die Autoren erhebliche Mühe gekostet hat.
Und nachdem das Problem erkannt ist, liegt eine Abhilfe nicht unmittelbar auf der Hand. Natürlich kann man eine große Menge unordentlicher Bilder erzeugen und dem Netz als Lernstoff vorlegen. Aber dabei steigt der Trainingsaufwand leicht auf das Tausendfache oder mehr, was die Sache unpraktikabel macht. Für eine wirksame Abhilfe braucht es wohl noch neue Ideen.
The post Die seltsamen Fehlleistungen neuronaler Netze originally appeared on the HLFF SciLogs blog.
