Monoeder, oder Hungerbühlers Gürteltier
Christoph Pöppe
Mathematiker und Mathematikerinnen neigen ähnlich wie Zoologen zuweilen dazu, ihre Gegenstände zu klassifizieren. Ein Polyeder ist zunächst nichts weiter als ein von ebenen Flächen begrenzter geometrischer Körper. Die Dinger können sehr verschieden aussehen, und so richtig viel kann man in dieser Allgemeinheit nicht über sie aussagen. Um einen Überblick zu gewinnen, teilt man sie in Klassen ein, die ihrerseits durch besondere Eigenschaften definiert sind.
Das Polyeder besteht aus lauter gleichen, regelmäßigen Vielecken? Dann ist es schon fast ein platonischer Körper, also eines der fünf sehr speziellen Polyeder, die schon in der griechischen Antike große Aufmerksamkeit genossen. Selbst der Philosoph Platon tat ihnen die Ehre an, sie in einem seiner Dialoge zu erwähnen – daher der Name.

Allerdings gibt es noch andere Möglichkeiten, gleiche, regelmäßige Vielecke zu Polyedern zusammenzufügen (weswegen die platonischen Körper zusätzlich die Bedingung erfüllen müssen, dass alle Ecken gleich aussehen). Am einfachsten ist es, zwei gleiche platonische Körper entlang einer Seitenfläche zusammenzukleben.

Aus Tetraedern kann man beliebig lange Ketten bauen, Oktaeder fügen sich zu Ringen zusammen, Ikosaeder lassen sich mit oktaederförmigen „Tunneln“ zu beliebig komplizierten Gebilden zusammensetzen. Man kann auch Würfel in beliebiger Menge aneinanderklatschen. Wenn es nur zwei von ihnen sind, dann verbinden sich zwei benachbarte Quadrate zu einem länglichen Rechteck, womit die Bedingung „regelmäßige Vielecke“ verletzt wäre; aber dem kann man aus dem Weg gehen, indem man die Klötze in jede Richtung kreuzförmig aneinandersetzt.

Alles ganz nett, aber ein Klassifizierer wird nicht richtig glücklich damit. Die Zusammensetzungen machen die Sache sehr unübersichtlich; und es sollte eigentlich genügen, sich mit deren Bestandteilen auseinanderzusetzen. Wie sieht es mit „elementaren“ Polyedern aus, also solchen, die sich nicht in kleinere Körper derselben Klasse zerlegen lassen? Was für „Monoeder“ gibt es, das heißt Körper, die von lauter gleichen Flächen begrenzt werden, wenn man diesen Flächen erlaubt, nicht regelmäßig (gleichseitig und gleichwinklig) zu sein?
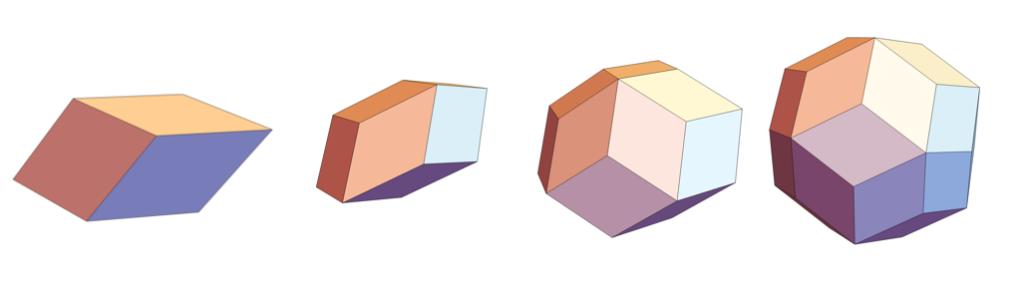
Allerlei. Die einfachste Methode, einen solchen zu erzeugen, geht so. Man stelle sich einen Würfel als Drahtgestell vor; genauer: Die Kanten sind lauter starre Stangen, aber an den Ecken sind sie frei gegeneinander verdrehbar. Man ziehe einen solchen Drahtwürfel an zwei genau gegenüberliegenden Ecken auseinander. Dadurch deformieren sich die Quadrate zu Rauten; wenn man es sorgfältig macht, sind diese Rauten alle gleich, und man erhält ein sogenanntes Rhomboeder. Sogar eine unendliche Schar von ihnen: Je nachdem, wie stark man zieht, geht das Ding von der Würfelform allmählich zu einem immer schlankeren Gebilde über, bis es in einer unendlich dünnen Spindel endet. Zusammendrücken statt Auseinanderziehen geht auch; dabei wird der ursprüngliche Würfel immer platter, bis er zu einem sechseckigen Pfannkuchen wird.
Unter diesen unendlich vielen Rhomboedern sind diejenigen einer näheren Betrachtung wert, die von so genannten „goldenen Rauten“ begrenzt werden. Das sind solche, deren Diagonalen im Verhältnis des Goldenen Schnitts (\(\tau=(\sqrt 5 +1)/2 \)) stehen; es gibt eine schlanke und eine platte Version. Mit ihnen kann man nämlich den Raum auf eine sehr spezielle Weise füllen, die einem dreidimensionalen Quasikristall entspricht. Obendrein gibt es weitere interessante Körper aus 12, 20 oder 30 goldenen Rauten.
Eine weitere Quelle für Monoeder sind die catalanischen Körper, so benannt nicht aufgrund irgendeines Bezugs zu Katalonien, sondern nach dem belgischen Mathematiker Eugène Charles Catalan (1814–1894). Es handelt sich um die Dualen zu den archimedischen (halbregelmäßigen) Körpern. Ihre Flächen sind drachenförmig und untereinander gleich, weil die Ecken der archimedischen Körper untereinander gleich sind.
An dieser Stelle geraten die Bemühungen der Polyeder-Zoologen ins Stocken. Gibt es über die oben genannten Rezepte hinaus ein allgemeines Verfahren, um Monoeder zu erzeugen oder auch nur einen Überblick über deren Vielfalt zu gewinnen? Das sieht im Moment nicht so aus. Umso willkommener ist da ein neues Rezept, das wir dem Mathematiker Norbert Hungerbühler von der ETH Zürich und seinem Studenten Marcel Pirron verdanken. Die zugehörige wissenschaftliche Arbeit (Nina Hungerbühler, Norbert Hungerbühler, Marcel Pirron: „New families of monohedral polyhedra“) ist noch nicht veröffentlicht; immerhin gibt es einen Zeitschriftenartikel zum Thema.
Die erste Idee ist: Man stelle zwei quadratische Spiegelkacheln aufrecht auf den Tisch, so dass sie sich entlang einer lotrechten Kante berühren; nennen wir sie die „Gemeinschaftskante“. In den Platz zwischen den beiden Spiegeln setze man lauter gleiche (kongruente) Vielecke, die einander entlang von Kanten treffen, wie das bei einem Polyeder üblich ist, und außerdem ein Stück der Gemeinschaftskante vor dem Blick des Betrachters vollständig verbergen. Das Flächenensemble hat also einen oberen und einen unteren Endpunkt auf der Gemeinschaftskante, und auf jedem Spiegel verläuft von einem Endpunkt zum anderen ein Weg, der vollständig aus Kanten des Ensembles besteht.
Wenn jetzt noch der Winkel zwischen den Spiegeln ein Teiler von 360 Grad ist, dann bilden das Flächenensemble, dessen Spiegelbilder in beiden Spiegeln sowie die Spiegelbilder der Spiegelbilder – und so weiter – zusammen ein vollständiges, geschlossenes Polyeder. Man muss allerdings in Kauf nehmen, dass die eigentlich gleichen Flächen in zwei Varianten vorkommen, die nur spiegelbildlich gleich sind.
Jetzt gilt es nur noch das Vieleck zu finden, das in der beschriebenen Weise mit seinesgleichen und seinen Spiegelbildern zusammenpasst. Es stellt sich heraus: Es geht mit einem Viereck in vier Exemplaren, zwei in der einen und zwei in der anderen Orientierung. Und dafür wiederum genügt es, sechs Punkte zu finden, zwei in der Luft und je zwei auf den Spiegeln, derart, dass sie die gemeinsamen Ecken der vier Vierecke bilden. Zwei weitere Punkte, nämlich den oberen und den unteren Endpunkt auf der Gemeinschaftskante, darf man „ohne Beschränkung der Allgemeinheit“ willkürlich vorgeben. Durch eine andere Wahl der Endpunkte ändern sich nämlich nur die Gesamtgröße des Gebildes sowie seine Position im Raum, und auf die kommt es nicht an.
An dieser Stelle kommt die Rechnerei ins Spiel. Die alten Griechen konnten die wesentlichen Größen der platonischen Körper mit Zirkel und Lineal konstruieren; aber das Verfahren ist hier aussichtslos. (Vielleicht funktioniert es in exotischen Ausnahmefällen; aber er wird sich schwerlich jemand bereit finden, auch nur darüber nachzudenken.) Vielmehr legt man in den ganzen Aufbau ein Koordinatensystem, möglichst bequem, was in diesem Falle darauf hinausläuft, dass die z-Achse entlang der Gemeinschaftskante verläuft und oberer und unterer Endpunkt die z-Werte 1 bzw. –1 haben. Die Koordinaten der Punkte auf den Spiegelflächen wählt man so, dass sie gar nicht anders können, als auf den Spiegelflächen zu liegen. Und die beiden Punkte in der Luft haben halt je drei unbekannte Koordinaten. Deren Anzahl wird jedoch dadurch verringert, dass für sie eine Symmetriebedingung gilt.
Damit hat man ein Sortiment unbekannter Zahlen, die gewisse Bedingungen erfüllen müssen. Die vier Punkte jedes Vierecks müssen in einer Ebene liegen; zahlreiche Seitenlängen müssen gleich sein, damit die Vierecke am Ende kongruent sind; und eine weitere Bedingung erzwingt, dass das ganze Gebilde nicht allzu schief wird. Alle diese Bedingungen lassen sich in Gleichungen formulieren, und am Ende hat man ein System von sieben Gleichungen für sieben Unbekannte.
Ein nichtlineares, wohlgemerkt. Wieso? Kurze, oberflächliche Erklärung: Alle Seitenlängen berechnet man über den Satz des Pythagoras, Sie wissen schon: \(a^2+b^2=c^2\), \(a\) und \(b\) sind die Abstände in Koordinatenrichtung, da gehen die Unbekannten ein, \(c\) ist die Größe, die eine Bedingung erfüllen muss. Man kann es so umformulieren, dass die Bedingung für \(c^2\) statt für \(c\) gilt, das erspart einem eine Quadratwurzel in der Gleichung, aber die Unbekannten, die in \(a\) und \(b\) eingehen, werden quadriert; schon hat man ein System von quadratischen Gleichungen, und dafür gibt es kein Standardverfahren.
Also lässt man sich auf ein numerisches Näherungsverfahren ein. In diesem Fall bietet sich das Newton-Verfahren an. Das hat zwar auch seine Tücken, aber wenn’s funktioniert, liefert es sehr rasch eine Lösung des Gleichungssystems mit beliebiger Genauigkeit. (Im nächsten Beitrag erzähle ich mehr darüber.) Und siehe da: Die erfolgreiche Anwendung des Verfahrens liefert nicht nur den Beweis, dass ein Monoeder aus Vierecken existiert, sondern auch dessen genaue Gestalt. Und das für jede Einstellung des Spiegelpaars!
Norbert Hungerbühler hat das für den sehr engen Winkel von 20 Grad zwischen den Spiegeln durchgerechnet. Das ergibt ein Monoeder aus 18 mal 4 = 72 Vierecken. Im Computerbild hat er es, gemeinsam mit seiner Tochter Nina, rot und von innen beleuchtet dargestellt und als „Rubin“ bezeichnet. Da ich Verständnisschwierigkeiten hatte, habe ich es nachgerechnet und aus steifem Papier „in echt“ nachgebaut. Ich gebe zu, mein Exemplar sieht nicht so edelsteinartig aus, sondern mehr wie ein Gürteltier. Vor allem muss es sich beim Basteln am Ende so zusammenrollen, wie ich es bei einem echten Gürteltier im Zoo beobachten konnte.

Ob mehr oder weniger glänzend: Der Zoo der Monoeder aus Vierecken hat reichlich Zuwachs bekommen. Ob damit das Sortiment vollständig ist? Wohl kaum. Im Dschungel der Polyeder gibt es mit Sicherheit auch von dieser speziellen Familie noch viel zu entdecken.
The post Monoeder, oder Hungerbühlers Gürteltier originally appeared on the HLFF SciLogs blog.