Nichtlineare Wellen und Solitonen
Christoph Pöppe
Es ist Zeit, die Zusage aus meinem letzten Beitrag einzulösen: Wie passen ein „ordentliches“ Verhalten und Nichtlinearität zusammen?
Lineare Systeme sind die braven, überschaubaren, diejenige, deren Verhalten man (im Allgemeinen) gut vorausberechnen kann. Dagegen sind die nichtlinearen die Chaoten: Mit ihnen kann alles Mögliche passieren, und mit der Vorhersagbarkeit sieht es schlecht aus, weil die kleinste Abweichung in den Anfangsdaten das Verhalten des Systems völlig verändern kann.
Wie kann aus nichtlinearen Verhältnissen Ordnung entstehen? Zwei Möglichkeiten hatte ich aufgeführt: Entweder ist das System „fast linear“, will sagen, einem linearen System so ähnlich, dass man den Unterschied außer Acht lassen kann – zumindest für eine Weile. Das ist der Grund, warum unser Kalender jedes Jahr im Wesentlichen gleich funktioniert: Das Planetensystem ist zwar im Prinzip chaotisch, aber das macht sich erst nach ein paar Millionen Jahren ernsthaft bemerkbar.
Oder viele chaotische Ereignisse wirken in ihrer Gesamtheit wie Zufall, und das Verhalten des Gesamtsystems ist aus statistischen Gründen sehr ordentlich. Das ist das, was im Kochtopf, allgemein in thermodynamischen Systemen, passiert.
Und dann gibt es dieses merkwürdige Phänomen, das Fermi, Pasta und Ulam bei ihren Computerexperimenten entdeckten: Lauter Massenpunkte sind durch nichtlineare Federn aneinandergekoppelt. Stößt man einen von ihnen an, so breitet sich eine Welle durch die Kette aus – so weit nichts Besonderes –, aber sie zerfließt nicht. Das würde nämlich bei linearen Systemen passieren, wenn sie nicht gerade so klinisch rein sind wie elektromagnetische Wellen im Vakuum.
Wie war das? Elektromagnetische Wellen in Materie, zum Beispiel Licht in Glas, verhalten sich noch ziemlich ordentlich; eine lineare Theorie beschreibt das ganz gut. Aber die Ausbreitungsgeschwindigkeit ist nicht mehr konstant, sondern hängt von der Frequenz ab. (Da war was: Brechungsindex = Verhältnis der Ausbreitungsgeschwindigkeiten ist abhängig von der Frequenz = Farbe der Lichtwelle, deswegen kann man mit einem Prisma das Licht in seine Spektralfarben zerlegen …) Ein einzelner, lokal begrenzter Stoß wäre als Überlagerung von gewöhnlichen Wellen verschiedener Frequenzen zu beschreiben, und wegen ihrer verschiedenen Geschwindigkeiten laufen die auseinander, das heißt, die an einer Stelle konzentrierte Erregung zerfließt. Das könnte man auch bei Wasserwellen beobachten; leider sind Wasseroberflächen zweidimensional, und die kreisförmige Welle, die ein eingeworfenes Steinchen hinterlässt, nimmt schon deswegen an Höhe ab, weil ihre Energie sich auf einen immer größer werdenden Kreis verteilt; gegen diesen Effekt fällt das Zerfließen nicht groß auf.
In einem engen Kanal bewegt sich das Wasser dagegen im Wesentlichen eindimensional. Wenn die Kielwellen der Schiffe allmählich kleiner werden, ist das echtes Zerfließen (ja, Reibungseffekte spielen wie immer auch eine Rolle). Umso bemerkenswerter ist es, wenn das nicht stattfindet! Deswegen wird noch heute gerne ein Mensch namens John Scott Russell zitiert, der 1834 beobachtete, wie von einem plötzlich angehaltenen Schiff eine einsame Welle sich löste und durch den Kanal wanderte. Russell folgte ihr zu Pferde über mehrere Meilen, ohne dass sich ihre Form nennenswert änderte.
Irgendeinen Effekt muss es geben, der eine vom Zerfließen bedrohte Welle wieder aufsteilt. Es dauerte immerhin bis 1895, bis die beiden Niederländer Diederik Korteweg und Gustav de Vries die Sache in eine mathematische Gleichung fassen konnten: eine nichtlineare partielle Differenzialgleichung, die zum Beispiel so aussieht: \[{\partial u \over \partial t} = 6u {\partial u \over \partial x} + {\partial^3 u \over \partial x^3} \] \(u\) ist die Höhe des Wassers über der Gleichgewichtshöhe, abhängig vom Ort \(x\) und der Zeit \(t\), und die Maßeinheiten sind gerade so gewählt, dass alle Vorfaktoren gerade gleich 1 bzw. 6 werden. Der Term \({\partial^3 u \over \partial x^3}\) macht das Zerfließen, und \(u {\partial u \over \partial x}\) macht das Aufsteilen.
Die Anwendbarkeit der Korteweg-de-Vries-Gleichung für echte Wasserwellen in Kanälen ist eher begrenzt. Die von Scott Russell beschriebene einsame Welle ist nicht wirklich häufig zu beobachten; und in der Tat mussten Korteweg und de Vries in ihrer Veröffentlichung sehr viele Annahmen machen, die anscheinend nicht immer erfüllt sind. Die Mathematiker dagegen fahren mittlerweile total auf die Gleichung ab. Man kann nämlich über ihre Lösungen eine große Menge von Aussagen treffen – vollkommen unerwartet für eine nichtlineare Gleichung.
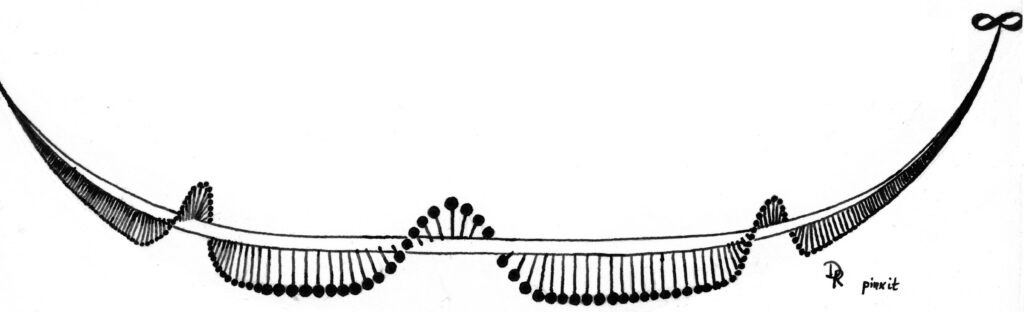
Es beginnt damit, dass es für die Gestalt der einsamen Welle eine explizite formelmäßige Darstellung gibt. Man setzt voraus, dass die Lösung der Gleichung sich in unveränderter Gestalt mit konstanter Geschwindigkeit bewegt, führt also ein mitwanderndes Koordinatensystem ein. Dann hängt die Lösung nicht mehr von der Zeit, sondern nur noch vom Ort ab, und die Gleichung vereinfacht sich zu einer gewöhnlichen Differenzialgleichung. Deren Lösung hatten schon Korteweg und de Vries gefunden. Sie hat im Wesentlichen die Form \[u(x)={1\over\cosh^2 x}= {4 \over (e^x+e^{-x})^2}\; .\] So sieht sie aus:

Es gibt sie in allen Größen. Je größer sie ist, desto steiler und zugleich schneller ist sie. Und wenn eine große einer kleinen begegnet, dann vereinigen sie sich nicht etwa, sondern die große überholt im Effekt die kleine. Hinterher sieht es, bis auf eine kleine Verschiebung, so aus, als wären sich die beiden nie begegnet.
Ein solches Verhalten beobachteten Norman Zabusky und Martin Kruskal 1965 bei Computersimulationen (seit den Zeiten von Fermi, Pasta und Ulam hatten die Geräte schon mächtig an Leistung zugelegt). Bei dem Versuch, die Ergebnisse dieser Simulationen durch eine Näherungsformel zu beschreiben, probierten sie herum – und stellten fest, dass ihre Formel eine weitere exakte Lösung der Gleichung beschrieb!
Das war nun eine echte Sensation. Wenn man zwei Lösungen einer nichtlinearen Gleichung addiert, kommt im Allgemeinen keine Lösung heraus – sonst wäre die Gleichung ja linear –, aber mit einer etwas komplizierteren Verknüpfung zweier elementarer Lösungen funktioniert das.
Wie man nun nachrechnen konnte, verhalten die beiden einsamen Wellen sich so, wie sich die theoretischen Physiker den Stoß zweier Billardkugeln vorstellen, die in ihrer Bewegungsfreiheit auf eine Gerade beschränkt sind. Von hinten kommt eine schnelle und stößt die langsamere an. Daraufhin tauschen die beiden Energie und Impuls aus, die bisher langsame läuft mit der Geschwindigkeit der bisher schnellen davon und umgekehrt.
Da sie sich also wie Teilchen verhalten und die Namen der Elementarteilchen (Proton, Neutron, Elektron …) auf „-on“ enden, wurden die einsamen Wellen („solitary waves“) kurzerhand „Solitonen“ getauft. Unter diesem Namen erlangten sie fortan eine erhebliche Berühmtheit. Sie tauchten nämlich in den verschiedensten Kontexten auf.
Der spätere Abel-Preisträger Peter D. Lax fand 1968 ein Kriterium, mit dem man bestimmen konnte, ob ein bestimmtes System Soliton-Eigenschaften aufweist. Und da fand sich so allerlei. Insbesondere gibt es ein System aus Massenpunkten und nichtlinearen Federn zwischen nächsten Nachbarn, das nicht nur ungefähr ein Soliton-System ist, sondern exakt. Nach seinem Entdecker Morikazu Toda heißt es Toda-Gitter („Toda lattice“). Und zwar ist die (abstoßende) Kraft, die eine Feder bei der Auslenkung \(\Delta x\) ausübt, proportional zu \(e^{-\Delta x}\). Sie drückt also ihre Endpunkte am intensivsten auseinander, wenn sie sehr komprimiert wird, und wird umso schlapper, je länger sie wird. Es ist etwas schwierig, sich eine physikalische Realisierung vorzustellen, selbst wenn man – was am Systemverhalten nichts ändert – zu jeder Federkraft eine Konstante addiert; aber das macht nichts. Auf jeden Fall ist das Kraftgesetz echt nichtlinear.
Ein anderes System haben sich die Quantenphysiker ausgedacht. Dass eine Welle und ein Teilchen eigentlich dasselbe sind, gehört ja zu den Grundideen der Quantenmechanik. Aber so, wie die Theorie formuliert ist, sagt die Wellenfunktion zu einem Teilchen nur, mit welcher Wahrscheinlichkeit man das Teilchen am Ort \(x\) vorfindet, wenn man nachmisst (und damit die schöne Wellenfunktion ruiniert). Eine solche Wellenfunktion kann niemals zwei miteinander interagierende Teilchen beschreiben; vielmehr benötigt die Theorie für diesen Fall neue Konstruktionen.
Wenn es aber so eine Wellenfunktion für mehrere Teilchen auf einmal gäbe, dann müsste die Gleichung, die ihre Zeitentwicklung beschreibt, nichtlinear sein, im Gegensatz zur linearen Schrödinger-Gleichung, die solches für die üblichen Wellenfunktionen tut. Eine solche Gleichung haben die Physiker tatsächlich gefunden. Ihre Gedankenspiele sind fern der Realität – wogegen nichts einzuwenden ist, man kann die Anpassung an die Realität ja nachholen, wenn man sich mit dem System etwas besser auskennt. In diesem Fall muss man vorläufig damit leben, dass der Raum nur eine Dimension hat.
So sieht die Gleichung aus: \[ {\partial^2 u \over \partial x^2}-{\partial^2 u \over \partial t^2}= \sin u \] Sie heißt „Sine-Gordon-Gleichung“ – wieder so ein Wortspiel. Es gibt eine Gleichung, die so ähnlich aussieht und nach ihren Entdeckern „Klein-Gordon-Gleichung“ genannt wird. Ersetzt man deren rechte Seite durch den Term mit dem Sinus, dann liegt die Benennung nahe, weil sich im Englischen „Klein“ auf „sine“ wie Sinus reimt.
Es gibt sogar ein mechanisches Modell, das die Sine-Gordon-Gleichung realisiert – zumindest in der Theorie. Man nehme ein unendlich langes Gummiband und spanne es waagerecht aus. In das Gummiband piekt man genau von unten lauter Stecknadeln Kopf an Kopf. Masse steckt nur in den Stecknadelköpfen, alles andere ist masselos. Das Gummiband hängt auch nicht durch; aber es ist torsionselastisch. Wenn man es in sich verdreht, wehrt es sich mit einer Rückstellkraft.
Den Zustand niedrigster Energie nimmt das System an, wenn alle Köpfe nach unten hängen. (Ja, es gibt ein konstantes Gravitationsfeld über die ganze unendliche Länge des Gummibands – ich sage doch, das Modell ist sehr theoretisch.) Aber man kann eine Kinke in das Gummiband machen, das heißt es so verdrillen, dass irgendwo die Stecknadelköpfe eine Runde um das Gummiband drehen und dann wieder brav abwärts hängen. Die Variable \(u(x)\) ist in diesem Modell der Winkel des Stecknadelkopfs an der Stelle \(x\) gegen die Ruhelage.
Diese Kinken sind die Solitonen der Sine-Gordon-Gleichung. Sie können das Gummiband entlangwandern, und wenn sie einander begegnen, tauschen sie Energie und Impuls aus wie die Massenpunkte im eindimensionalen Billard. Zu allem Überfluss gibt es rechtsgedrehte und linksgedrehte Kinken. Wer denkt da nicht an Teilchen und Antiteilchen? Allerdings: Wenn sie einander begegnen, vernichten sie sich nicht gegenseitig, sondern durchdringen einander und wandern weiter. Sonst würden Gesamtenergie und -impuls nicht erhalten bleiben.
Es gibt übrigens eine Grenzgeschwindigkeit. In den gewählten Maßeinheiten, die wieder jeden Vorfaktor verschwinden lassen, hat sie den Wert 1. Schneller als diese „Lichtgeschwindigkeit“ kann kein Soliton sich bewegen, und wenn es sich dieser Geschwindigkeit nähert, wird es zusammengedrückt – relativistische Längenkontraktion. Sogar ein bisschen Relativitätstheorie steckt in dieser schlichten Gleichung.
Korteweg-de Vries, Sine-Gordon, Toda – das sind nur drei prominente unter zahlreichen Systemen, die Solitonverhalten zeigen und damit einerseits nichtlinear, andererseits auf verblüffende Weise „ordentlich“ sind. Wenn die linearen Systeme die Elefanten sind, was sind dann die Soliton-Systeme zoologisch gesehen? Es stellt sich heraus: Sie sind mit den Elefanten auf eine merkwürdige Weise verwandt. Aber das erzähle ich Ihnen beim nächsten Mal.
The post Nichtlineare Wellen und Solitonen originally appeared on the HLFF SciLogs blog.