Penrose und die Parkette
Christoph Pöppe
„Penrose? Das ist doch der mit den Müsterchen“, simste mir meine Tochter. Über die hatte sie nämlich vor vielen Jahren eine Art Seminararbeit in der Schule angefertigt. Was diese geometrischen Formen denn bitte mit den schwarzen Löchern zu tun hätten, für die der Typ jüngst den Physik-Nobelpreis gekriegt hat?
Die schlichte Antwort lautet: gar nichts. Roger Penrose ist so genial, dass er in einem Thema bahnbrechende Ergebnisse erzielt – und sich dann auf das nächste stürzen kann, ohne von irgendwelchen eigenen Vorarbeiten profitieren zu müssen. So hat er nicht nur gemeinsam mit seinem britischen Landsmann Stephen Hawking die Theorie der Schwarzen Löcher ein bedeutendes Stück vorangebracht, sondern auch gemeinsam mit seinem britischen Landsmann John Horton Conway die Theorie der nichtperiodischen Pflasterungen. Und dass er auch zum Konzept der Pseudoinversen, immerhin ein zentraler Begriff der numerischen linearen Algebra, wesentliche Beiträge geleistet hat – na ja, bei einem Menschen seines Ranges ist das dann eine eher nebensächliche Fußnote.
Während die Schwarzen Löcher nicht zum Anfassen, sondern – zum Glück – weit von uns entfernt sind, haben die nichtperiodischen Pflasterungen nicht nur wenige Jahre nach der Theorie eine physikalische Realisierung gefunden – in Form der Quasikristalle –, sie sind auch mit Buntstiften und Papier nachvollziehbar. (Oder mit entsprechender Computergrafik.)
Wie kommt man auf so etwas? Zum Beispiel indem man spielerisch mit regelmäßigen Fünfecken die Fläche zu füllen versucht. Mit Drei-, Vier- oder Sechsecken ist das sehr einfach. Mit Siebenecken kann es nicht gehen. Sie sind so dick und rund, dass, wenn man zwei von ihnen aneinandersetzt, ein drittes nicht mehr dazwischenpasst. Und das wird mit höheren Eckenzahlen nur noch schlimmer.

Es bleibt das Fünfeck. Zu dick ist es nicht. Drei von ihnen passen mühelos um einen Punkt. Aber es bleibt so ein dreieckiger Zwickel dazwischen, mit dem man nicht recht etwas anfangen kann. Was tun? Man kann beschließen, mit dem Zwickel zu leben und im Übrigen die Fläche möglichst dicht mit Fünfecken zuzupflastern. Wenn man das einigermaßen ordentlich macht, ergänzen sich stets zwei Zwickel zu einer schmalen Raute mit dem Öffnungswinkel 36 Grad. Ganz nett, aber ein bisschen langweilig.

Oder man verzichtet auf die Forderung, dass das Fünfeck regelmäßig (gleich lange Seiten, gleiche Winkel) sein soll. Damit macht man ein riesengroßes Fass auf: Es stellt sich heraus, dass es 15 wesentlich verschiedene Arten gibt, die Ebene mit lauter gleichen Fünfecken zu bedecken. Die Entdeckung dieser Pflasterungstypen ist eine Geschichte für sich, voller Erfolge und Enttäuschungen: Immer wieder entdeckt jemand einen neuen Typ, ist fest davon überzeugt, damit das Problem endgültig erledigt zu haben, und muss sich Jahre später eines Besseren belehren lassen. Der Beweis, dass das mittlerweile bekannte Sortiment tatsächlich vollständig ist, wurde erst vor wenigen Jahren geführt.
Aber bleiben wir beim regelmäßigen Fünfeck; und wenn wir schon so einen Wert auf Regelmäßigkeit legen, versuchen wir doch, die Symmetrie unseres Pflastersteins auf das ganze Muster zu übertragen. Gerade beim Fünfeck geht da eine Menge.
Setzen wir zum Beispiel die Zwickel nicht so ordentlich parallel, sondern so, dass sie sich zum Fünfstern ergänzen (links im Bild). Diese elegant geschwungenen Dreiergruppen von Fünfecken möchten irgendwie verlängert werden, und siehe da: Man kann aus den dreien einen Zehnerring machen (Mitte). Und schon ist der Stern von fünf Zehnerringen umgeben; das sieht ganz schnuckelig aus.
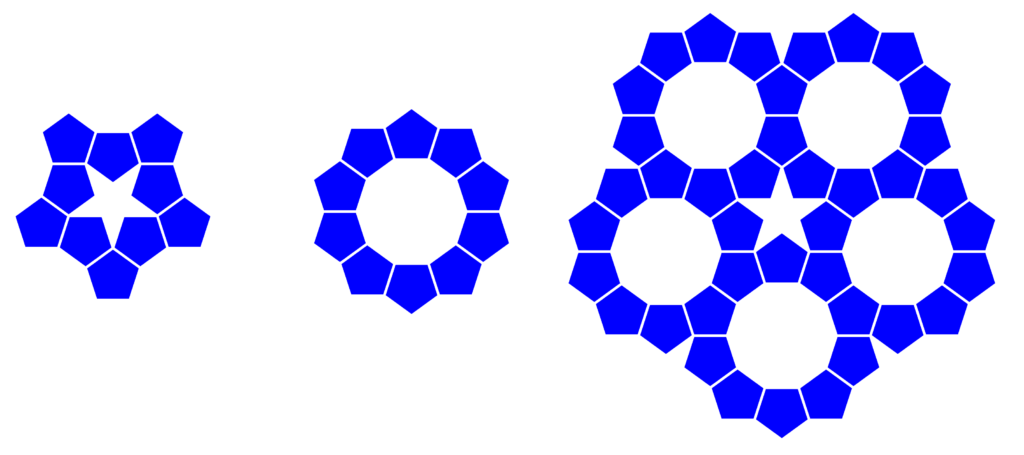
An der Außenseite des Musters tun sich wieder Zwickel auf, die wollen zu Sternen ergänzt werden:
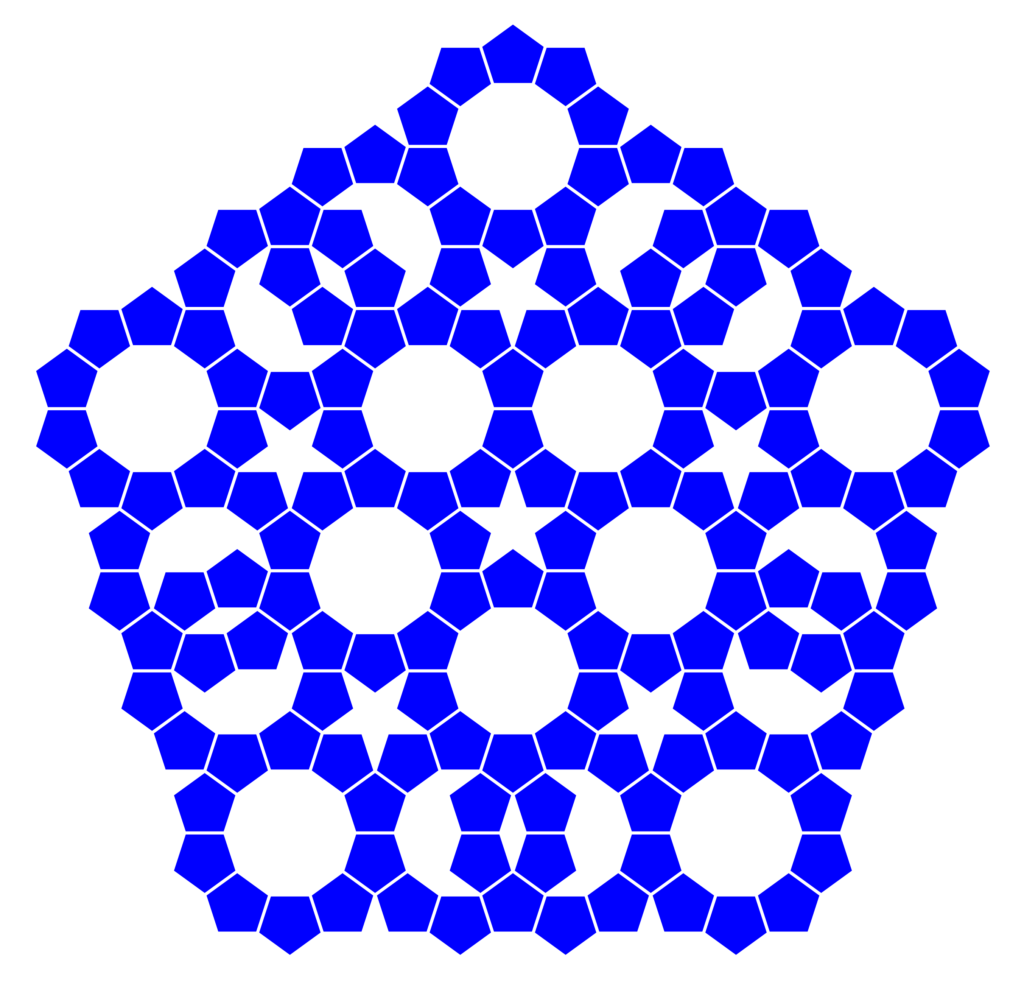
Das kann man auch noch einen Schritt weiter treiben:
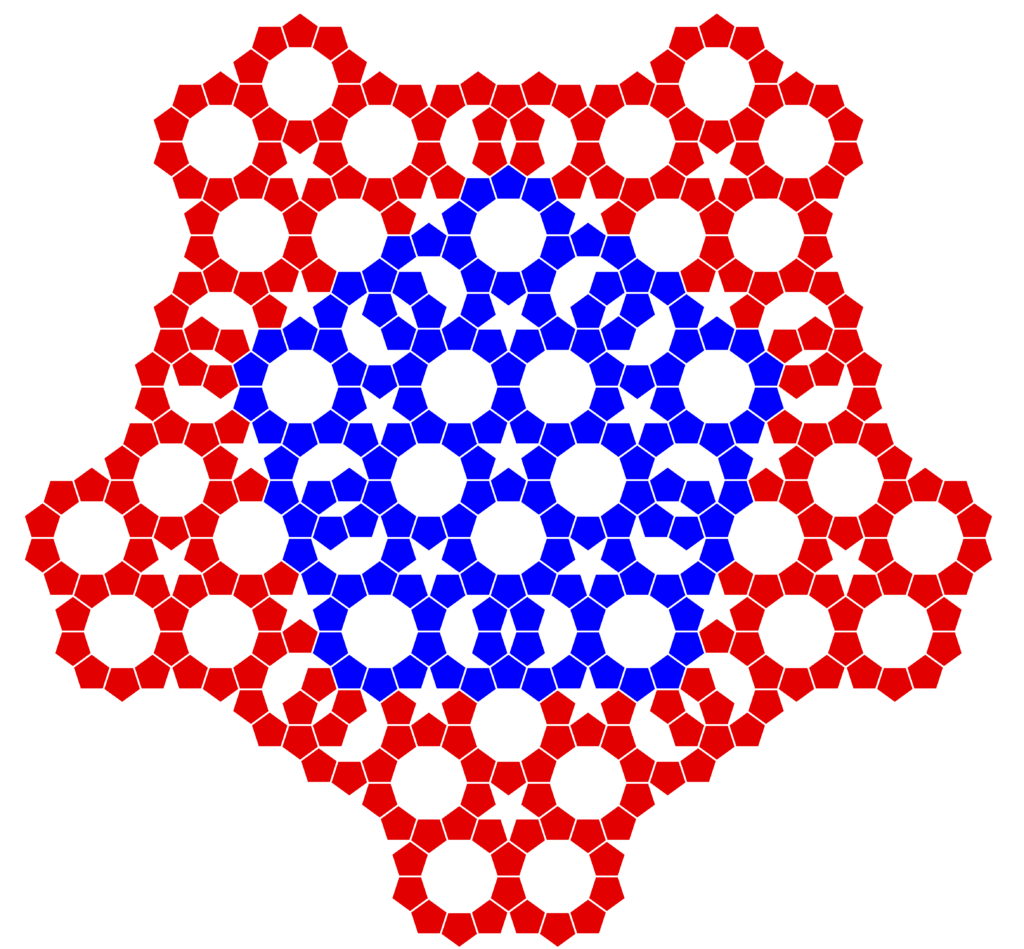
Spätestens jetzt fangen die zehneckigen Löcher doch etwas an zu stören, vor allem weil an manchen Stellen die Löcher von anderen Zehnerringen durchkreuzt werden. Außerdem ging es ja eigentlich darum, möglichst viele Fünfecke in der Ebene unterzubringen. Dem Problem ist abzuhelfen: In ein Zehneck passen drei Fünfecke – allerdings in zehn verschiedenen Orientierungen. Und im Allgemeinen kann man ein Zehneck nicht so füllen, dass die neu eingesetzten Fünfecke Teil eines Zehnerrings werden. Also: Aufbau nach einer strengen Regel funktioniert nicht; vielmehr hat man etwas Willkür im System, womit Unordnung zu befürchten ist. Ich habe die Zehnecke nicht ganz ohne Willkür, aber immerhin so gefüllt, dass die Fünfersymmetrie bezüglich des Sterns im Zentrum gewahrt bleibt.
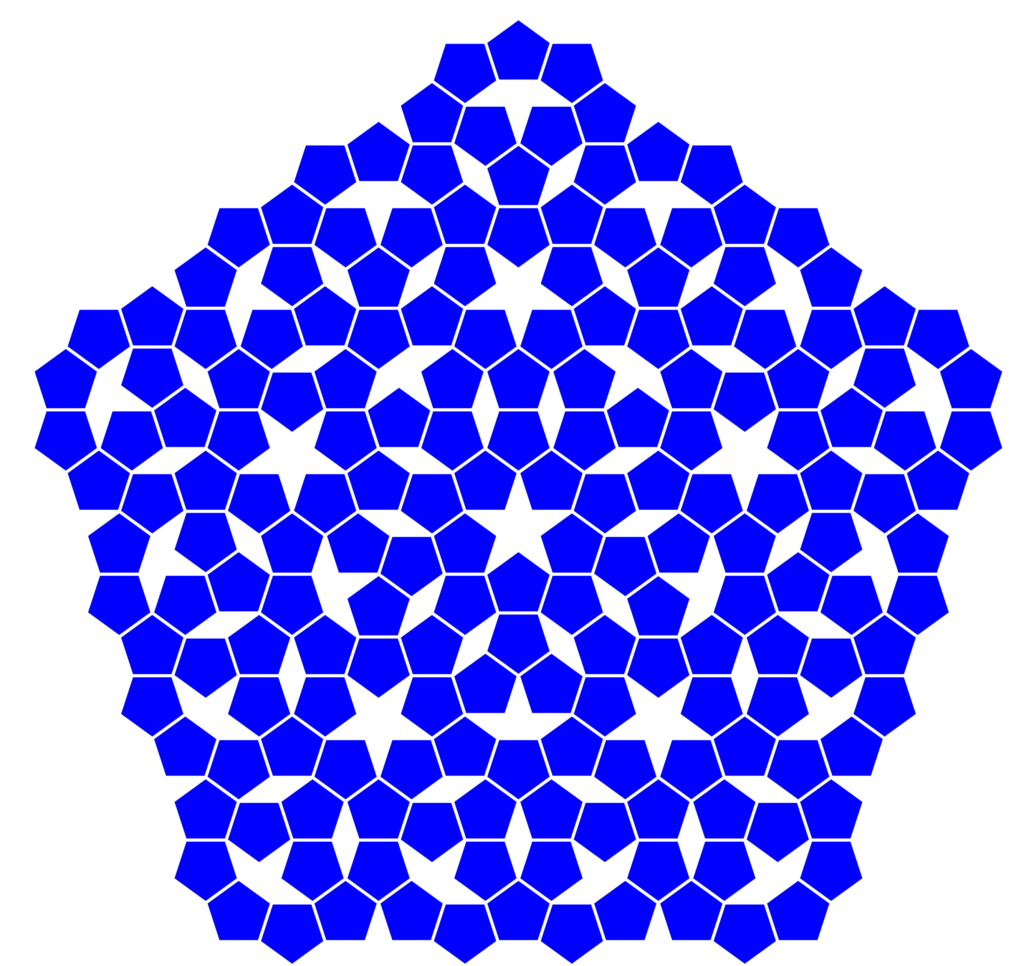
Wer auf diese Weise sein Badezimmer kacheln möchte, braucht vier verschiedene Sorten Fliesen: Fünfecke, Fünfsterne, schmale Rauten und „Schiffchen“ (sie sehen ja tatsächlich so aus wie die Papierschiffchen, die man den Kindern zu falten pflegt). Interessanterweise kann man eine zweite, kleinere Größe Fünfsterne ins Spiel bringen, indem man in jedes Fünfeck einen Stern einsetzt:

Was ein solcher kleiner Stern von „seinem“ Fünfeck übrig lässt, sind fünf Dreiecke. Jedes von ihnen ergänzt sich mit dem Kollegen vom Nachbarfünfeck zu einer breiten Raute mit dem Öffnungswinkel 72 Grad. Und die Dreiecke, die keinen Partner finden, weil sie an ein weißes Feld (schmale Raute, Schiffchen oder großer Fünfstern) grenzen? Siehe da, man kann sie in etwas kleineren Fünfecken unterbringen. Dabei werden auch die weißen Felder komplett überdeckt, und schon hat man eine Parkettierung aus kleinen Fünfsternen (gelb), dicken Rauten (schwarz) und kleinen Fünfecken (grün und violett, je nach Orientierung). Das Bild unten zeigt einen Ausschnitt aus dem obigen Muster, links vor, rechts nach der (teilweisen) Ersetzung:
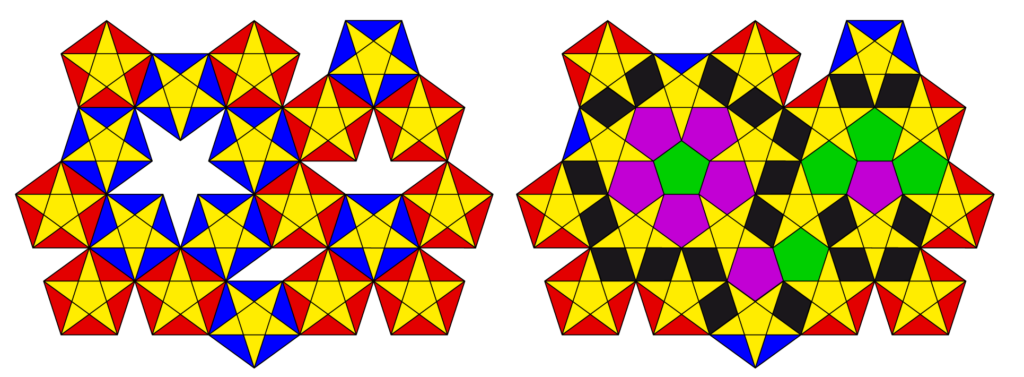
So kann man noch eine ganze Weile weiterspielen, und das haben auch ziemlich viele Leute getan. Sogar von Johannes Kepler – jawohl, dem mit den Kepler’schen Gesetzen der Planetenbewegung – sind entsprechende Skizzen überliefert. Wer sich damit beschäftigt, kommt unweigerlich auf das Sortiment der Formen, die dabei eine Rolle spielen: Fünfeck, Fünfstern, Zehneck, dünne Raute, dicke Raute und Schiffchen. Dabei treten gewisse Formen in mehreren Größen auf, und große und kleine Form stehen in demselben Verhältnis zueinander wie Diagonale und Seite eines regelmäßigen Fünfecks. Es handelt sich um die berühmte Verhältniszahl des Goldenen Schnitts, \( \tau= ( \sqrt5+1)/2 \approx 1{,}618\ldots\) . Und: Es ist nicht von vornherein klar, ob man ein begrenztes Muster im selben Geiste fortführen kann. Vielleicht passiert einem ja wieder so ein Konflikt wie oben, als es nicht möglich war, die Zehnerringe vor Eindringlingen zu bewahren.
So weit kommt man in der Erforschung der Fünfecksmuster auch ohne besondere Genialität. Aber nun treten Penrose und Conway auf den Plan. Es gelingt ihnen nicht nur, das unübersichtliche Sortiment der Parkettsteine auf zwei elementare Formen zu reduzieren. Sie finden auch Vorschriften, die bestimmen, auf welche Weisen man Parkettsteine aneinanderlegen darf („Anlegeregeln“ oder auch ”matching rules“). Ein vorschriftsmäßig gelegtes Parkett kann nie langweilig (korrekt ausgedrückt: periodisch) werden. Es kann also kein begrenztes Stück Parkett geben, das man mit verschobenen Kopien seiner selbst vorschriftsmäßig zu einer Überdeckung der ganzen Ebene machen könnte. Und schließlich erarbeiten sie ein überaus mächtiges theoretisches Werkzeug, das einen ganzen Wissenschaftszweig etabliert: das Substitutionsprinzip.
Aber der Reihe nach.
Die beiden elementaren Steine, die Penrose und Conway in die Forschung einführten, sind der „Pfeil“ („dart“, links) und der „Drachen“ („kite“, rechts).
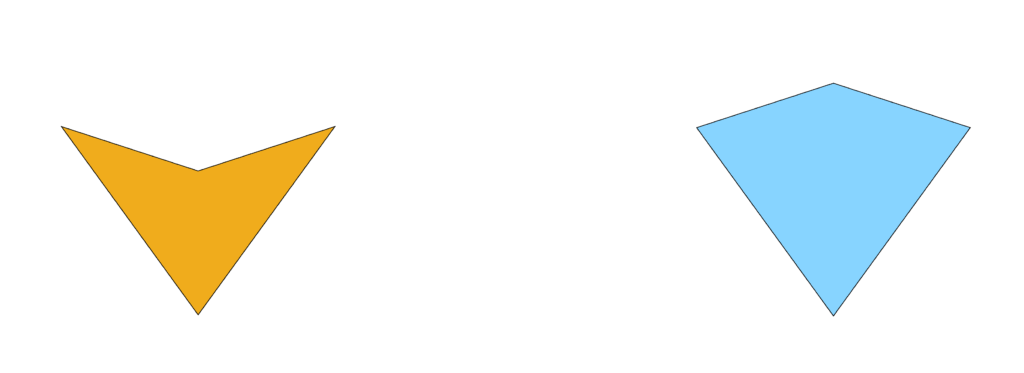
Jeder von ihnen ist zusammengesetzt aus zwei gleichschenkligen Dreiecken, deren lange Seite sich zur kurzen verhält wie \(\tau\) zu 1, das Verhältnis des Goldenen Schnitts. Diese „goldenen Dreiecke“ gibt es in genau zwei Sorten, „breite“ mit zwei kurzen und einer langen Seite und „hohe“ mit zwei langen und einer kurzen. Der Pfeil besteht aus zwei breiten goldenen Dreiecken und der Drachen aus zwei hohen.

Die zugehörigen Anlegeregeln lassen sich zum Beispiel durch Kreisbögen ausdrücken: Die Steine dürfen nur so zusammengesetzt werden, dass jeder Kreisbogen auf der anderen Seite der Fuge seine Fortsetzung findet. Das sieht dann zum Beispiel so aus:

Unteres Bild aus der Achtklassarbeit von Almut Pöppe (heute Almut Gatz), 1995
Was sich im Prinzip bis ins Unendliche fortsetzen lässt. Aber einfach Steine vorschriftsmäßig an ein bestehendes Stück Parkett anlegen funktioniert nicht. Nur allzu leicht gerät man in eine „Sackgasse“, also eine Lücke, in die unter keinen Umständen ein Stein passt. Um unendliche Parkette zu konstruieren, musste Penrose noch Theorie nachschieben.
Das beginnt mit der Feststellung, dass Drachen und Pfeil nicht die einzigen geeigneten Paare von Pflastersteinen sind. Man kann zwei hohe und zwei breite Dreiecke auch anders zusammensetzen; dabei ergeben sich zwei alte Bekannte: die dünne und die dicke Raute.
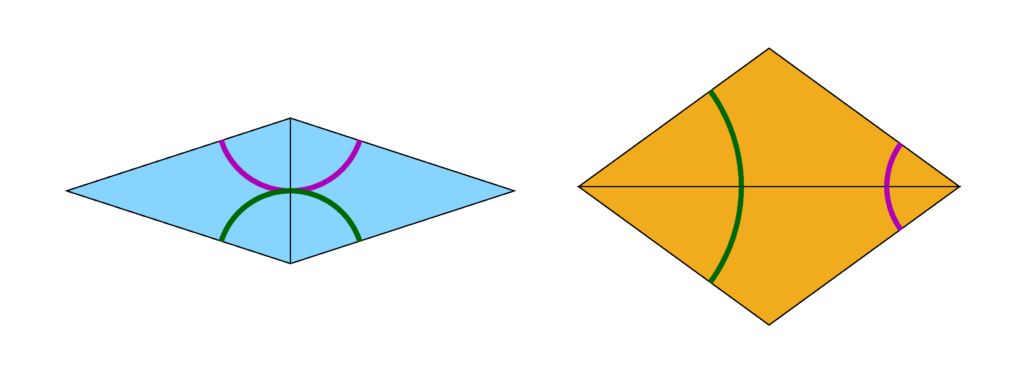
Wieder gibt es Anlegeregeln, und wieder kann man unter Beachtung dieser Regeln ein garantiert nichtperiodisches Parkett legen:
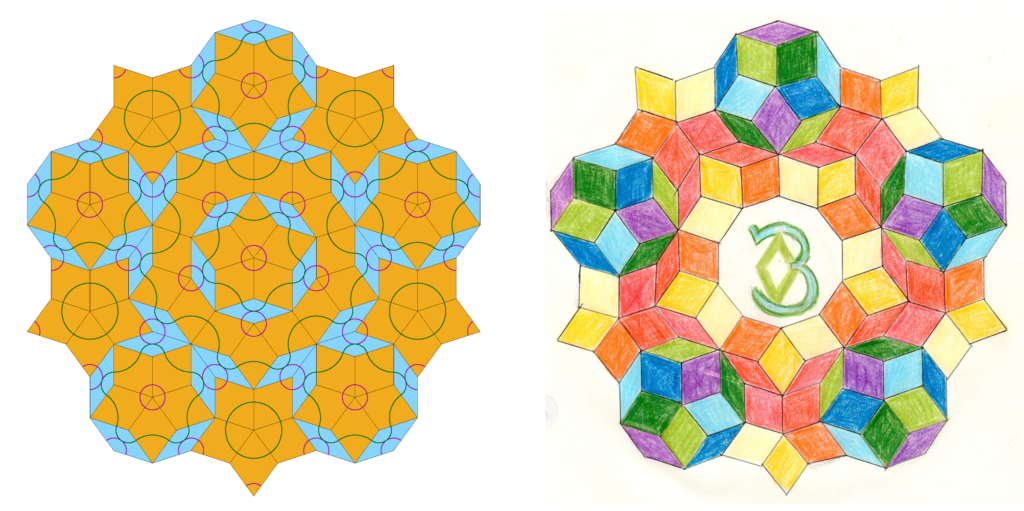
Rechtes Bild aus der Achtklassarbeit von Almut Pöppe (heute Almut Gatz), 1995
Diese Sorte Parkett ist allgemein unter dem Namen „Penrose-Parkett“ bekannt.
Schließlich stellt sich heraus, dass die theoretisch ergiebigsten Steine weder Drachen und Pfeil noch die beiden Rauten sind, sondern die eher unscheinbaren Teile, aus denen beide zusammengesetzt sind: die goldenen Dreiecke. Ein hohes goldenes Dreieck ist nämlich zerlegbar in ein breites und ein kleines hohes, und ein breites zerfällt in ein kleines hohes und ein kleines breites.

Warum funktioniert das? Weil die Seiten der Dreiecke im Verhältnis \(\tau\) des Goldenen Schnitts stehen; entsprechend ist der Verkleinerungsfaktor gleich \(1/\tau = 1-\tau \), und alles passt. Die erste Zerlegungsregel macht aus dem Drachen eine dünne Raute plus zwei breite Dreiecke.
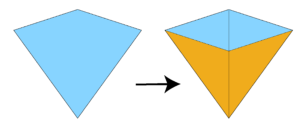
Und in einem Drachen-Pfeil-Parkett findet sich dank den Anlegeregeln neben jedem dieser breiten Dreiecke ein ebensolches, mit dem es sich zu einer dicken Raute ergänzt. Die erste Zerlegungsregel macht aus einem Drachen-Pfeil-Parkett ein Rautenparkett!
Die zweite Zerlegungsregel macht aus einer dicken Raute – ja, was genau?

Es sieht aus wie ein Drachen und ein Pfeil. Aber das wäre mit den Anlegeregeln nicht vereinbar. Die richtige Antwort ist: ein Pfeil und zwei halbe Drachen. Wieder sorgen die Anlegeregeln dafür, dass jedes hohe Dreieck neben sich einen Partner hat, mit dem es sich zum Drachen ergänzt.
Insgesamt wird durch die Anwendung beider Zerlegungsregeln aus einem Rautenparkett wieder ein Rautenparkett mit verkleinerten Rauten. (Für das Drachen-Pfeil-Parkett kann man ebenso argumentieren.) Jetzt ist man natürlich frei, das neue Parkett mit dem Faktor \(\tau\) zu vergrößern. Dadurch bedeckt es eine größere Fläche als das alte. Und wenn man es geschickt anstellt, dann ist das alte sogar ein Teil des neuen, so dass das neue als echte Erweiterung des alten gelten kann.
Die ganze Prozedur aus Zerlegen und Vergrößern („Substitution“, ältere Bezeichnung: „Inflation“) kann man nun beliebig oft wiederholen und gewinnt damit beliebig große Parkette – im Grenzwert pflastert man damit die ganze unendliche Ebene.
Damit ist die Substitution ein probates Mittel, um unendlich große Parkette zu erzeugen – was durch schrittweises Anwenden der Anlegeregeln eben im Allgemeinen nicht funktioniert. Wichtiger noch: Man kann das Substitutionsverfahren rückwärts anwenden („Deflation“). Aus vielen kleinen Steinen macht man dadurch wenige große oder am Ende einen einzigen. Auf diesem Weg findet man eine Fülle von theoretischen Aussagen über nichtperiodische Pflasterungen der Ebene.
Inzwischen gibt es zu diesem Thema eine schier überwältigende Menge an Beispielen. Schauen Sie in die Tilings Encyclopedia, die Dirk Frettlöh und seine Kollegen von der Universität Bielefeld zusammengetragen haben. Die Augen werden Ihnen übergehen!
Zum Thema dieses Textes gibt es ein hervorragendes (englischsprachiges) Video: „The Infinite Pattern that Never Repeats“.
The post Penrose und die Parkette originally appeared on the HLFF SciLogs blog.