Potenzreihen und Konvergenzkreise
Christoph Pöppe
Nach längerer Pause will ich mich jetzt beeilen, dem Lobpreis der komplexen Zahlen und der holomorphen Funktionen das dritte wesentliche Teilstück hinzuzufügen: die Sache mit der unendlichfachen Differenzierbarkeit, mehr noch: der Entwickelbarkeit in eine Potenzreihe.
Diesmal geht es gewissermaßen tief in den Maschinenraum der Mathematik, da, wo man sich manchmal an den öligen Zahnrädern die Finger schmutzig macht – zum Beispiel an dem Begriff der Differenzierbarkeit, den Sie vielleicht noch aus der Schule kennen und sich nicht so recht mit ihm anfreunden konnten; er ist ja wirklich etwas sperrig. Wenn Sie sich mit Potenzreihen auskennen, werden Sie am Ende alte Bekannte wiedertreffen.
Wie war das? Differenzierbar ist, wenn die Kurve eine Tangente hat. Tangente ist, wenn sie sich an die Kurve so eng anschmiegt wie überhaupt möglich. Das ist schon richtig. Aber was heißt das genau?
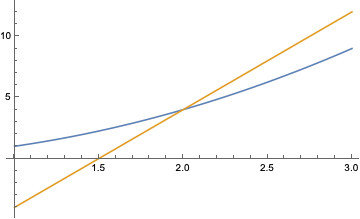
Hier Kurve, da Gerade. Kurve \(f(x)=x^2 \) und Gerade \(g(x)=8x-12\) treffen sich in einem Punkt, und zwar (2, 4). Wenn man mit \(x\) langsam auf den Punkt \(x=2\) zuwandert, geht die Differenz \(f(x)-g(x)\) gegen null. Kein Wunder, wenn die beiden sich in \(x=2\) treffen. Aber eine Tangente ist \(g\) offensichtlich nicht.
So sieht eine richtige Tangente aus:
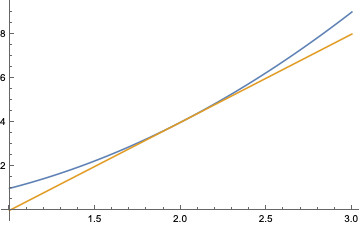
Die Idee ist, dass die Differenz \(f(x)-g(x)\) „schneller“ gegen null geht als die Differenz \(x-2\). Das wiederum wäre zu präzisieren zu der Aussage, dass \(f(x)-g(x)\) selbst dann noch gegen null geht, wenn man es durch \(x-2\) (was ja auch gegen null geht) dividiert. Mit ein bisschen Umrechnen kommt dann die übliche Definition heraus, nämlich dass \( (f(x)-f(2))/(x-2) \) einem endlichen Grenzwert zustrebt, den man dann die Ableitung von \(f\) an der Stelle 2 oder kurz \(f’(2)\) nennt.
Hier will ich auf einen anderen Aspekt hinaus: Die Tangente ist die beste Möglichkeit, die Kurve anzunähern, wenn man nur Geraden, sprich lineare Funktionen zur Auswahl hat. Die Annäherung ist richtig gut in der Nähe des speziell dafür ausgewählten Punktes, in unserem Beispiel \(x=2\), und wird mit zunehmender Entfernung schlechter – beliebig schlecht, um genau zu sein, denn die Tangente in dem speziellen Punkt hindert die Kurve nicht, weiter draußen die wildesten Sprünge zu vollführen.
Was heißt „in der Nähe“, und was heißt „weit draußen“? Das weiß man nie so genau. Die ganze Definition bleibt ja abstrakt und sagt erst einmal nichts darüber, wie viele Zentimeter lang die Näherung noch gut bleibt. (Wir wissen noch nicht einmal, ob die \(x\)-Werte überhaupt in Zentimeter gemessen werden!) Um dieses Problem präzise zu fassen, verwendet man die (gewöhnungsbedürftige) Epsilon-Delta-Definition, was hier nicht weiter vertieft werden soll.
Wie kann man die Näherung an die Funktion verbessern? Immer in der Nähe eines speziellen Punktes, der ab jetzt \(x_0\) heißen soll? Indem man das Sortiment der zur Näherung verwendbaren Funktionen vergrößert. Zum Beispiel indem man außer linearen auch quadratische Näherungsfunktionen zulässt. Die sind immerhin krumm und deswegen bereit, sich noch enger an eine krumme Funktion anzuschmiegen.
Oder man genehmigt sich nicht nur die erste und die zweite Potenz von \(x\), sondern die dritte; damit kommt man Funktionen bei, die sich mal linksherum und mal rechtsherum krümmen, die vierte, die noch größeres Gehampel mitmacht, die fünfte …
Mit jeder Potenz, die man hinzunimmt, wird die Näherung besser – kein Wunder, schlechter kann es ja nicht werden. Wenn die neu hinzugekommene Möglichkeit unter allen Umständen die Sache schlechter machen würde, könnte man sie ja mit dem Faktor null versehen und wäre wenigstens so gut wie zuvor.
Das wirklich Schöne an der ganzen Annäherei ist: Es gibt ein einfaches Kochrezept, um die jeweils optimale Menge an Zutaten zu bestimmen. Man nehme \(a_0\) Gramm von der konstanten Funktion \(f_0(x)=1\), \(a_1\) Gramm von der linearen Funktion \(f_1(x)=x-x_0\), \(a_2\) Gramm von der quadratischen Funktion \(f_2(x)=(x-x0)^2\) und so weiter, addiere die alle zusammen, und fertig ist die Näherung. Denn die Zutatenmengen („Koeffizienten“) \(a_0, a_1, a_2, \dots\) sind leicht auszurechnen: \(a_n = f^{(n)}(x_0) / n!\) Die \(n\)-te Zutat (die natürlich nicht in Gramm gemessen wird) ist gleich der \(n\)-ten Ableitung unserer Funktion \(f\) in dem Punkt \(x_0\), geteilt durch \(n!\) (\(n\)-Fakultät), das Produkt aller natürlichen Zahlen von 1 bis \(n\).
Diese Fakultätsfunktion wächst rasant an, schneller als jede Potenz von \(n\). Das heißt, die Zutatenmengen werden mit zunehmendem \(n\) sehr schnell immer kleiner – vorausgesetzt, die Werte der \(n\)-ten Ableitungen halten sich einigermaßen in Grenzen. Und natürlich vorausgesetzt, es gibt sie überhaupt. Schon die Differenzierbarkeit ist eine ziemlich spezielle Eigenschaft einer Funktion, und ob deren Ableitung ebenfalls differenzierbar ist, die Funktion also überhaupt eine zweite Ableitung hat, ist nicht von vornherein klar. Und so weiter. Zu jeder Bedingung, die man gerne erfüllt sehen würde, findet sich ein Gegenbeispiel.
Eigentlich sind also die Funktionen, deren erste, zweite, dritte … Ableitungen sämtlich existieren, geradezu exotische Ausnahmeerscheinungen. Aber in der mathematischen Praxis laufen sie einem die ganze Zeit über den Weg. Und zwar diejenigen, die nicht nur unendlich oft differenzierbar sind, sondern bei denen die nach obigem Rezept zubereitete Näherungsfunktion (sie heißt übrigens „Taylorpolynom“) auch tatsächlich funktioniert. Selbst dafür gibt es Gegenbeispiele.
Was genau heißt es, dass die Näherung durch ein Taylorpolynom optimal ist? Dass der Unterschied zwischen Funktion und Näherung schneller gegen null geht als die höchste Potenz von \(x-x_0\), die unter den Zutaten des Taylorpolynoms vorkommt. Und wenn das für jedes Taylorpolynom der Fall ist, dann darf man „unendlich viele Zutaten zusammenschütten“ und erhält nicht nur eine Näherung an die Funktion, sondern eine exakte Darstellung der ganzen Funktion.
Na ja. Wenn es unendlich viele Summanden zu addieren gibt, läuft das auf einen Grenzwert hinaus, dann will wieder bewiesen werden, dass er existiert, und um ihn auszurechnen, muss man manchmal erheblich um die Ecke denken. Aber zumindest der Existenzbeweis ist in diesem Fall nicht besonders problematisch. Unsere unendliche Summe (die „Taylorreihe“) lautet ausgeschrieben
\[ f(x)=\sum_{n=0}^\infty {f^{(n)}(x_0) (x-x_0)^n \over {n!} }\; ,\] und solche unendlichen Summen pflegen zu konvergieren – das heißt, es gibt einen endlichen Grenzwert, der als Wert der Summe gelten kann –, wenn die einzelnen Summanden hinreichend schnell klein werden. Zum Kleinwerden trägt einerseits die große Zahl \(n!\) im Nenner bei, andererseits der Faktor \( (x-x_0)^n\); denn wenn \(x\) nahe bei \(x_0\) liegt, also der Betrag von \(x-x_0\) klein ist, dann gehen seine Potenzen gegen null wie eine geometrische Folge. Das hilft bis zu einem gewissen Grad sogar, wenn die Ableitungswerte \(f^{(n)}(x_0)\) mit zunehmendem \(n\) gegen unendlich gehen.
Genauer: Es gibt für jede Taylorreihe einen Maximalabstand \(r\), den „Konvergenzradius“. Wenn der Betrag \(|x-x_0|\) kleiner als \(r\) ist, konvergiert sie; ist er größer als \(r\), konvergiert sie nicht, und wenn er gleich \(r\) ist, weiß man es nicht so genau.
Insbesondere darf der Konvergenzradius unendlich sein. Dann passiert etwas sehr Merkwürdiges: Das Verhalten der Funktion auf der ganzen reellen Achse ist bestimmt durch ihr Verhalten in einem einzigen Punkt \(x_0\)! In einer beliebig kleinen Umgebung dieses einzigen Punktes, um genau zu sein, denn es kommt auf den Wert der Funktion und aller ihrer Ableitungen in diesem Punkt an, und die Ableitungen sind ja Grenzwerte, in die Funktionswerte in der Nähe von \(x_0\) eingehen. Also muss man, um die Funktion vollständig zu kennen, das gedachte Fernrohr nicht nur auf den Punkt \(x_0\) richten, sondern muss sich eine beliebig kleine Umgebung von \(x_0\) mit anschauen.
Analytische Funktionen, das sind solche, deren Taylorreihe überall konvergiert, haben sozusagen einen starken inneren Zusammenhalt. Man kann nicht an einer Stelle ein bisschen wackeln, ohne die ganze restliche Funktion in Mitleidenschaft zu ziehen – wenn sie analytisch bleiben soll.
Auch wenn die Taylorreihe überall konvergiert, wird die Konvergenz typischerweise um so mühsamer, je weiter man sich von dem speziellen Punkt \(x_0\) entfernt. Das wird deutlich an Funktionen, die zwar analytisch sind wie die Sinusfunktion, aber sich vollkommen anders verhalten als jedes Polynom.
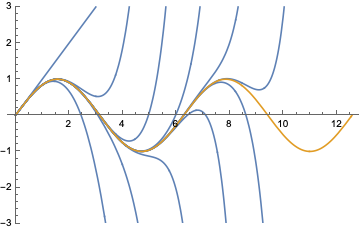
Die Sinusfunktion (braun im Bild) bewegt sich brav zwischen 1 und –1 und kreuzt dabei unendlich oft die \(x\)-Achse. Polynome dagegen haben das so an sich, dass sie für große Werte von \(x\) gegen unendlich gehen; und ein Polynom vom Grad \(n\) kann auch höchstens \(n\)-mal die \(x\)-Achse kreuzen. Entsprechend haben die ersten paar Taylorpolynome (blau im Bild) die größte Mühe, sich der Sinusfunktion anzupassen.
Und wenn eine Funktion an irgendeiner Stelle unendlich wird, kann es dort keine Konvergenz mehr geben. Nehmen wir \(f(x)=1/(1-x) \). An der Stelle \(x=1\) wird der Nenner null, der Funktionswert ist dort also nicht definiert, und in seiner Nähe geht es rasant gegen unendlich. Vielleicht kennen Sie die Potenzreihe dieser Funktion noch aus der Schule. Es gilt \(f(x) = 1 + x + x^2 + x^3 + \dots \), das folgt aus der Summenformel für die geometrische Reihe. Und die konvergiert bekanntlich nur, wenn \(|x|\), der Betrag von \(x\), kleiner als 1 ist.
Aber was ist mit einer Funktion wie \(f(x)=1/(1+x^2)\)?
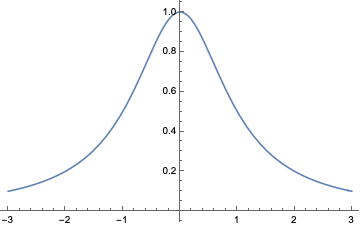
Die ist nun wirklich das Paradebeispiel eines Schlaffis. Ewig lang passiert nichts; einmal im Leben, in der Nähe von \(x=0\), rafft sie sich zu einer gewissen Aktivität auf, um dann alsbald wieder nachzulassen und in alle Ewigkeit monoton auf die Null zuzuschleichen. Von Unendlichkeitsstelle keine Spur. Da sollte doch die Taylorreihe kein Problem haben, dieses friedliche Wesen wiederzugeben, weniger jedenfalls als mit der Sinusfunktion. Aber weit gefehlt! Der Konvergenzradius ist 1, wie bei ihrer wilden Schwester \(1/(1-x)\).
Wieso? Hier hilft ein Blick auf die komplexen Zahlen. Ich habe zwar die ganze Zeit nur von reellen Funktionen geredet; aber das lässt sich alles ohne nennenswerte Änderungen auf komplexe Werte von \(x\) und \(f(x)\) übertragen. Dann ergibt auf einmal der Begriff „Konvergenzradius“ einen Sinn, denn in der komplexen Ebene ist es tatsächlich ein Kreis, in dem die Taylorreihe konvergiert.
Im Komplexen läuft unsere Schlaffifunktion zu großer Form auf; denn für \(x=\pm i\) wird \(x^2=-1\), der Nenner wird null, und unsere Funktion hat an diesen beiden Stellen Pole; so nennt man diese milde Form von Unendlichkeitsstelle. Der Konvergenzkreis mit Mittelpunkt null stößt bei \(\pm i\) sozusagen auf eine natürliche Grenze, über die hinaus er nicht wachsen kann.
Philosophische Schlussbemerkung: Selbstverständlich ist es legitim, sich ausschließlich mit reellen Funktionen zu beschäftigen und von komplexen Zahlen nichts wissen zu wollen, vor allem für einen Menschen, der die Mathematik auf reale Gegenstände anwenden will. Seltsamerweise bleiben dabei Fragen offen („Wieso ist der Konvergenzradius von \(1/(1+x^2)\) so klein?“).
Diese Fragen finden eine elegante Antwort, wenn man sich auf komplexe Zahlen einlässt. Eigentlich ist das Grund genug, sich ihnen zuzuwenden.
The post Potenzreihen und Konvergenzkreise originally appeared on the HLFF SciLogs blog.