Soliton-Gleichungen und die überraschende Rolle der Fredholm-Determinanten
Christoph Pöppe
Nach einigen eher allgemeinen Gedanken über lineare und nichtlineare Differenzialgleichungen und einer ersten Begegnung mit einer speziellen Art der letzteren, den „Soliton-Gleichungen“, will ich Ihnen dieses Mal endlich erzählen, wie die beiden zusammenhängen. (Ich hätte selber nicht gedacht, dass auf dem Weg zu diesem Ergebnis so viele Blümchen am Wegesrand stehen, die zumindest einen kurzen Blick wert sind …)
Wie war das? Die linearen Probleme sind nach einem verbreiteten Spruch wie die Elefanten unter den Tieren: Sie verfügen über etliche spezielle Eigenschaften, die sie uns besonders sympathisch machen. Vor allem kommt man mit der Lösung dieser Probleme sehr weit, die Summe zweier Lösungen ist wieder eine Lösung (Superpositionsprinzip), und einiges mehr. Aber im Übrigen sind sie auch nur eine Spezies im sehr unübersichtlichen Zoo aller Probleme, und irgendwelche Gemeinsamkeiten unter den nichtlinearen Problemen zu suchen – abgesehen davon, dass es sich nicht um Elefanten handelt – ist eigentlich vergebliche Liebesmüh.
Und dann gibt es Probleme, die definitiv keine Elefanten sind, aber mit diesen merkwürdige Gemeinsamkeiten haben – nennen wir sie Klippschliefer. Die possierlichen Tierchen dieses Namens zeigen bei der DNA-Analyse Merkmale von Verwandtschaft mit den Elefanten; aber ansehen kann man ihnen das beim besten Willen nicht. Die Klippschliefer-Probleme (offizieller Name: Soliton-Gleichungen) zeigen ein nichtlineares Superpositionsprinzip: Man kann Lösungen nicht einfach zu neuen Lösungen addieren, aber irgendwie überlagern kann man sie doch, mit dem Effekt, dass sich die elementaren Lösungen, die „Solitonen“, so zueinander verhalten wie Massenpunkte, die mit Energie und Impuls ausgestattet sind und auf der reellen Achse aufeinanderballern wie Billardkugeln.
Darüber hinaus verfügen Soliton-Gleichungen über eine Fülle interessanter Eigenschaften, darunter eine mit dem etwas optimistischen Namen „Integrabilität“. „Integrabel“ ist in diesem Kontext zu verstehen als „lösbar“; und in der Tat gibt es für integrable Systeme ein Lösungsverfahren. Aber das darf man nicht so verstehen, dass man einem Computer den Anfangszustand eines Systems eingibt, und der spuckt ganz laplace-dämonmäßig eine Formel aus, die den Systemzustand für alle Zeiten beschreibt. Vielmehr verläuft der Weg vom Anfangswert zur Lösung für alle Zeiten über lineare Hilfsprobleme, und da man die lösen kann, ist der Weg gangbar; es kommt halt im Allgemeinen keine explizite Formel dabei heraus.
Die Idee ist ungefähr folgende: Ich kenne einen Klippschliefer jetzt (sagen wir zum Zeitpunkt \(t=0\)) und will wissen, wie es ihm in Zukunft ergehen wird. Einfach so ausrechnen kann ich es nicht, denn der Klippschliefer ist nichtlinear. Aber zu jedem Klippschliefer gibt es genau einen Elefanten, und umgekehrt. Da Elefanten linear sind, ist ihre Zukunft leicht berechenbar. Also berechne ich zum Klippschliefer in seinem Anfangszustand den zugehörigen Elefanten, finde dessen zukünftige Zustände und berechne aus diesen die jeweils zugehörigen Zustände des Klippschliefers. Fertig!
Damit das funktioniert, kommt es entscheidend auf die Abbildung (oder auch Funktion, was im mathematischen Sprachgebrauch dasselbe ist) an, die aus einem Klippschliefer einen Elefanten macht, und natürlich auf deren Umkehrfunktion. Linear ist sie nicht; ein doppelter Klippschliefer ergibt keinen doppelten Elefanten. Aber ihre Berechnung verläuft über die Lösung eines linearen Hilfsproblems.
Stellen wir uns zum Beispiel als den Klippschliefer zum Zeitpunkt \(t=0\) so eine Lösung der Korteweg-de-Vries-Gleichung (zum Zeitpunkt \(t=0\)) vor, und zwar mit umgekehrtem Vorzeichen, damit das Folgende einleuchtender wird:
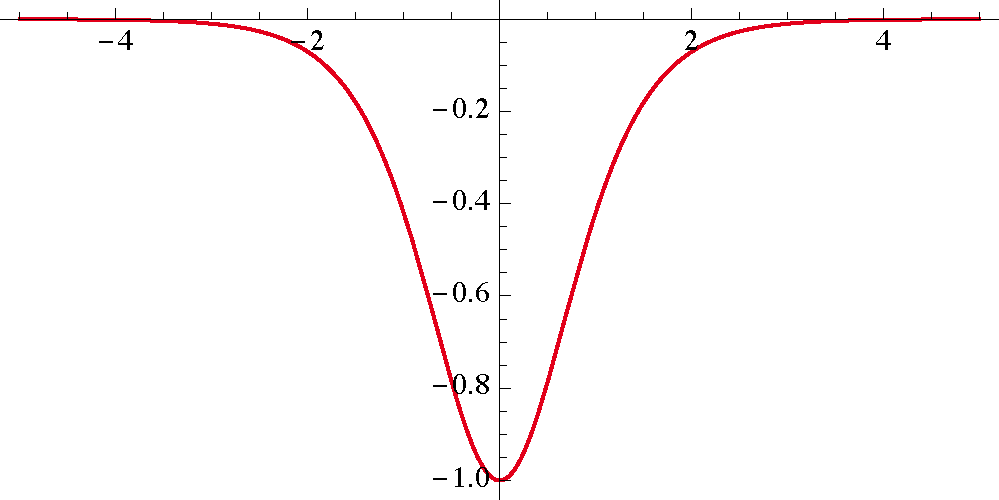
Diese Funktion interpretieren wir jetzt als das elektrische Potenzial eines Atomkerns. Was soll das? Das eine hat doch mit dem anderen nichts zu tun. In der Tat: Die Funktion war bisher (mit umgekehrtem Vorzeichen) die Höhe einer Wasserwelle in einem Kanal, deren Bewegung ist etwas völlig anderes als das, was einem Elektron in der Nähe eines Atomkerns passiert, und da gibt es auch keinen tiefsinnigen Zusammenhang.
Diese willkürlich erscheinende Interpretation dient vielmehr als etwas merkwürdige Lösungshilfe. Das Schicksal des Elektrons kann man ausrechnen, es handelt sich – kaum noch wiederzuerkennen – um eine Anwendung der Schrödingergleichung, die ist linear, und aus den Ergebnissen dieser Rechnung basteln wir uns unseren Elefanten zusammen.
Im Einzelnen: Das Elektron kann „in diesen Potenzialtopf hineinfallen“, das heißt vom Atomkern eingefangen werden und dort eines von mehreren möglichen Energieniveaus einnehmen. Oder das Elektron ist als Welle aufzufassen – wir sind in der Quantenmechanik – und wird am Atomkern „gestreut“, das heißt teilweise durchgelassen und teilweise reflektiert. Die Gesamtheit der Lösungen dieses Hilfsproblems nennt man die „Streudaten“; das sind die Reflexions- und Transmissionskoeffizienten in Abhängigkeit von der Wellenlänge sowie die diskreten Energieniveaus (für Fachleute: die Eigenwerte des linearen Operators \(\partial_x^2+V\), wobei \(V\) das Potenzial ist).
Jetzt kommt der Knüller: Folgt das „Potenzial“ der Korteweg-de-Vries-Gleichung, so folgen die Streudaten einer linearen, leicht zu lösenden Gleichung. Insbesondere bleiben die Eigenwerte unverändert. Für andere Soliton-Gleichungen nehmen etwas andere Streuprobleme die Rolle des linearen Hilfsproblems ein, aber allgemein gilt: Auf dem Weg über dieses Hilfsproblem macht man aus einem Klippschliefer einen Elefanten, das heißt aus einem ziemlich speziellen nichtlinearen Problem ein lineares.
Jetzt müssen wir nur noch vom Elefanten zurück zum Klippschliefer, das heißt, zu der Funktion, die eine Funktion (Lösung des nichtlinearen Problems) auf eine andere Funktion (Lösung des linearen Problems) abbildet, die Umkehrfunktion finden. Das findet man als das inverse Streuproblem („inverse scattering problem“) in der Literatur.
Der erste Schritt ist noch relativ unproblematisch. Man macht aus den Streudaten einen Integraloperator, der seinerseits vom Ort \(x\) abhängt. Das erfordert einen erheblichen theoretischen Aufwand, ist aber in der Sache nichts weiter als ein Blick auf den Elefanten aus ungewohnter Perspektive.
Nun betritt ein Konzept aus einer ganz anderen Ecke der Mathematik die Bühne: die Determinante. Eigentlich ist sie in der linearen Algebra zu Hause; das ist die Kunst, lineare Gleichungssysteme mit vielen Unbekannten zu lösen. In der Schule wird man mit zwei, allenfalls drei Unbekannten konfrontiert; aber die Verfahren, die man dabei anwendet, lassen sich auf beliebige Anzahlen verallgemeinern.
Das Wesentliche eines linearen Gleichungssystems steckt in seiner Matrix; das ist eine Zahlentabelle aus \(n\) Zeilen für \(n\) Gleichungen und \(n\) Spalten für \(n\) Unbekannte (man braucht im Allgemeinen genau so viele Gleichungen wie Unbekannte). Die Matrix ihrerseits verkörpert eine lineare Abbildung vom \(n\)-dimensionalen Raum in den \(n\)-dimensionalen Raum, und die Determinante ist eine einzige Zahl, die man aus allen Einträgen der Matrix ausrechnet. Wenn sie ungleich null ist, dann ist die Abbildung umkehrbar, und das Gleichungssystem hat in jedem Fall eine Lösung.
Die Praktiker mögen die Determinante nicht besonders. Sie auszurechnen ist nur geringfügig weniger Aufwand, als gleich das ganze Gleichungssystem zu lösen, und wenn man sie trotzdem ausrechnet, mit Gleitkommaarithmetik und den unvermeidlichen Rundungsfehlern, dann ist die Frage, ob sie gleich null ist oder nicht, eigentlich nicht zu beantworten.
Aber darum geht es in unserem Kontext gar nicht. Vielmehr denkt man über die Determinante des oben genannten Integraloperators nach. Der ist zwar eine lineare Abbildung – soweit alles in Ordnung –, aber er bildet Funktionen auf Funktionen ab; das heißt, er lebt in einem unendlichdimensionalen Funktionenraum. Die Determinante einer gewöhnlichen Matrix ist eine Summe von Produkten von Tabelleneinträgen; demnach wäre die Determinante eines Integraloperators eine unendliche Summe von unendlichen Produkten – wenn man denn den Integraloperator überhaupt als unendliche Matrix darstellen könnte. Da sind offensichtlich zunächst die Voraussetzungen zu klären, unter denen es so etwas überhaupt gibt. Das hat der schwedische Mathematiker Ivar Fredholm (1866–1927) Anfang des 20. Jahrhunderts getan, weswegen diese Objekte Fredholm-Determinanten heißen.
Nach der langen theoretischen Vorarbeit kommt der Lohn der Mühe jetzt überraschend schnell. Der Elefant ist – aus geeigneter Perspektive betrachtet – ein Integraloperator, der linear vom Ort \(x\) und der Zeit \(t\) abhängt. Dessen Fredholm-Determinante ist eine Zahl, die ebenfalls von \(x\) und \(t\) abhängt. Für sie hat sich der Name \(\tau\)-Funktion („Tau-Funktion“) eingebürgert. Aus ihr lässt sich der Klippschliefer durch eine einfache Umrechnung ermitteln. Im Fall der Korteweg-de-Vries-Gleichung lautet sie \[u(x,t) = 2 {\partial^2 \over \partial x^2} \log \tau(x,t) \; .\] Und das Schönste: Wenn die Streudaten nur aus den diskreten Energieniveaus im Potenzialtopf (den „Eigenwerten“) bestehen, dann wird der Integraloperator endlichdimensional! Die Fredholm-Determinante wird zu einer gewöhnlichen Determinante, und die kann man explizit ausrechnen. Es stellt sich heraus, dass jeder Eigenwert einem Soliton entspricht.
Damit hat man ein Mittel an der Hand, um jede Menge Lösungen der Soliton-Gleichungen explizit hinzuschreiben. Mehr noch: Auf lange Sicht geben diese „reinen N-Soliton-Lösungen“ das Wesentliche vom Verhalten dieser Systeme wieder. Denn während jedes Soliton auf einen engen Raumbereich konzentriert bleibt, verteilt sich der ganze Rest auf die Dauer gleichmäßig über die \(x\)-Achse und verschwindet dadurch in der Bedeutungslosigkeit. Darüber hinaus erlaubt die explizite Darstellung durch (gewöhnliche oder Fredholm-)Determinanten eine Fülle von Aussagen über Soliton-Systeme.
Jetzt kommt die disclosure: Die Sache mit den Fredholm-Determinanten ist mein Werk. Vor fast 40 Jahren habe ich die Methode entwickelt, erst für die Sine-Gordon-Gleichung, dann für die Korteweg-de-Vries-Gleichung. Andersherum wäre es einfacher gewesen: Die Korteweg-de-Vries-Gleichung ist der Analyse ziemlich direkt zugänglich, während man für Sine-Gordon noch ein paar Winkelzüge extra machen muss. Wie man vielleicht gemerkt hat, bin ich heute noch davon begeistert, wie das alles so schön zusammenpasst und wie die zahlreichen Arbeiten anderer Wissenschaftler, auf denen ich aufgebaut habe, sich in das Konzept mit den Determinanten fügen.
Die Begeisterung der Fachwelt hielt sich damals in engen Grenzen. Umso erfreulicher finde ich es, dass meine alten Arbeiten neuerdings häufiger zitiert werden. Und um das zu begreifen, was die gegenwärtigen Autoren aus meinen damaligen Ergebnissen machen, muss ich mir noch richtig Mühe geben.
The post Soliton-Gleichungen und die überraschende Rolle der Fredholm-Determinanten originally appeared on the HLFF SciLogs blog.