Von der Gefräßigkeit der Spitzmäuse und der Dauer des menschlichen Lebens

Christoph Pöppe

Es war im Jahre 1962. Mit der damals neuen Substanz Lysergsäurediethylamid (LSD) durfte man noch experimentieren, und die Psychologen Louis J. West und Chester M. Pierce aus Oklahoma City versuchten mit ihrer Hilfe jenem seltsamen aggressiven Erregungszustand namens Musth auf die Spur zu kommen, der periodisch junge Elefantenbullen zu befallen pflegt. Man wusste bereits, dass eine Dosis von 0,1 Milligramm pro Kilogramm Körpergewicht beim Menschen halluzinationsartige Zustände auslöst, während bei der Katze nur mit Mühe überhaupt eine Reaktion zu bemerken war. Dementsprechend injizierten sie dem 3000 Kilogramm schweren Elefanten Tusko knapp 300 Milligramm LSD. Fünf Minuten später konnte sich das Tier nicht mehr auf den Beinen halten, verfiel in krampfhafte Zuckungen und geriet in Atemnot. Hektische Versuche, ihm mit einem Gegenmittel aufzuhelfen, zeigten wenig Erfolg, und nach anderthalb Stunden war der Elefant tot.

Knapp 60 Jahre später stößt nicht nur die Kaltschnäuzigkeit übel auf, mit der die beiden Forscher in ihrem Artikel das missratene Experiment beschreiben, sondern auch die Tatsache, dass sie es schon damals besser hätten wissen können. Große Tiere leben langsamer als kleine. Während eine Spitzmaus täglich so viel fressen muss, wie sie selbst wiegt, um zu überleben, kommt ein fünf Tonnen schwerer Elefant mit bescheidenen 200 bis 300 Kilogramm pro Tag aus. Alles ist langsamer an ihm: Bewegung – relativ zur Körpergröße –, Herzschlag, Schwangerschaft, das ganze Leben – ein Elefant wird wesentlich älter als eine Maus – und eben auch die Stoffwechselintensität. Seine Leber baut das LSD so viel langsamer ab, dass es seine schädlichen Wirkungen viel intensiver entfaltet, in diesem Fall mit tödlichem Ausgang.

Wer das in einigermaßen exakte Zahlen fassen will, verwendet als Messgröße den Grundumsatz (basic metabolic rate): Energieverbrauch pro Zeiteinheit eines erwachsenen Tiers, das sich nicht bewegt und nicht verdaut, zu bestimmen über die Menge des im Messzeitraum ausgeatmeten Kohlendioxids. Es handelt sich im Wesentlichen um den Energieaufwand, den das Tier treibt, um seine Körpertemperatur aufrechtzuerhalten. (Hier und im Folgenden geht es ausschließlich um Säugetiere, auch wenn einige Forschende ihre Betrachtungen auf andere Tierarten und sogar Pflanzen ausdehnen.) Damit sind die nächsten Überlegungen schon ziemlich vorgezeichnet. Energieproduktion ist proportional der Körpermasse, Energieverlust, genauer: Wärmeabstrahlung, ist proportional der Körperoberfläche. Nehmen wir die Körperlänge L als grundlegenden Maßstab, so ist die Körpermasse proportional L³ und die Oberfläche proportional L². Damit Energieproduktion und -abstrahlung sich die Waage halten, muss der Grundumsatz G nicht der Masse M, sondern der Oberfläche proportional sein. Also: G ist proportional M ^2/3.

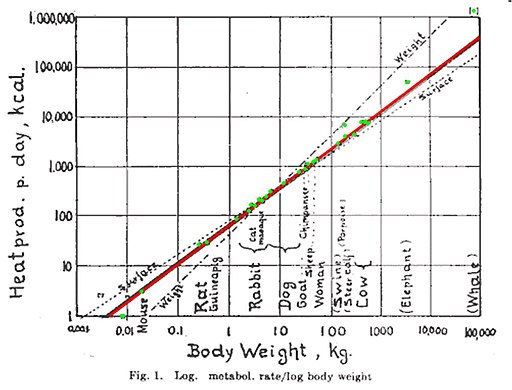
Klingt einleuchtend, ist aber falsch. Bereits 1947 hat der Physiologe Max Kleiber in Davis (Kalifornien) G und M für verschiedene Säugerarten einschließlich des Menschen gemessen und in ein Diagramm eingetragen (siehe unten). Dabei ergibt sich, dass der Exponent nicht gleich 2/3, sondern vielmehr gleich 3/4 ist.

Wie ist das zu verstehen? Man nimmt die Gleichung G =cM ^b; dabei ist c ein Proportionalitätsfaktor, der uns nicht weiter interessiert, und b der „allometrische Exponent“, das ist die Zahl, die eigentlich 2/3 hätte sein sollen. Man wendet auf die Gleichung die Logarithmusfunktion an: log G = log c + b log M, trägt die Datenpunkte (log M, log G ) in das Diagramm ein und findet mit einem Standardverfahren („Methode der kleinsten Quadrate“, „least squares fit“) die Gerade, die am besten zu den Datenpunkten passt. Deren Steigung ist der allometrische Exponent b. Kleiber hat in sein Diagramm auch die Geraden zu b=2/3 („surface“) und b=1 („weight“) eingetragen; da passt die rote zu b=3/4 wirklich besser.

Aber wie ist das zu erklären? Wenn die Welt vierdimensional wäre und „Oberflächen“ in ihr dreidimensional, dann wäre der allometrische Exponent 3/4 das Einleuchtendste von der Welt. Ist aber leider nicht so. Immerhin wissen wir, dass die Sache mit der Wärme nicht die entscheidende ist. Offensichtlich gelingt es den Tieren, die Diskrepanz zwischen Wärmeproduktion und -abstrahlung auf andere Weise zu überbrücken, zum Beispiel mit dichtem Mäusefell und großen kühlenden Elefantenohren.

Vielleicht besteht ja das wesentliche Problem nicht darin, die Energie – in Form von Wärme – loszuwerden, sondern sie überhaupt erst ans Ziel zu bringen, sprich: Sauerstoff und Glukose an jeden Punkt des Körpers zu transportieren. Dazu verwenden alle Säuger den Blutkreislauf: einen reich verzweigten Baum von der Aorta bis hin zu den feinsten Blutgefäßen, den Kapillaren. Die Astgabeln dieses Baums sehen an jeder Stelle des Baums – bis auf die absolute Größe der Äste – ungefähr gleich aus, eine Eigenschaft, die man als Selbstähnlichkeit bezeichnet. Und damit landet man unversehens bei der „fraktalen Geometrie der Natur“, um den Titel eines berühmt gewordenen Buches von Benoît Mandelbrot zu zitieren.

Die Idee ist: Man nähere – zum Beispiel – das System der Arterien nicht durch eine Sammlung von irgendwie zylindrischen Röhren an, sondern durch ein idealisiertes mathematisches Objekt (ein „Fraktal“), in dem die Verzweigung in immer kleinere Äderchen bis ins Unendliche weitergeht. Mit Hilfe dieser Näherung gewinnt man Aussagen über Eigenschaften des Systems, die auf klassisch-geometrischem Weg nicht oder nur äußerst mühsam zu haben sind. (Wie war das mit der Summe einer geometrischen Reihe? Die Formel für unendlich viele Glieder ist deutlich einfacher als die für endlich viele.)

Auf diesem Wege haben Geoffrey B. West, James H. Brown und Brian J. Enquist 1997 in einer viel beachteten Veröffentlichung Kleibers Gesetz, sprich den allometrischen Exponenten 3/4, hergeleitet. Die Einzelheiten sind überraschend kompliziert. Man muss unterstellen, dass ab einer gewissen Verzweigungstiefe im Aderbaum der pulsierende Blutstrom in einen laminaren übergeht. Für letzteren gilt das Gesetz von Hagen-Poiseuille mit dem Effekt, dass eine Ader vom halben Durchmesser nicht etwa ein Viertel des Blutstroms transportieren kann, wie es ihrem Querschnitt entspräche, sondern nur ein Sechzehntel. Zusätzlich geht in die Überlegungen ein, dass die Größe einer Körperzelle, insbesondere die eines roten Blutkörperchens, nicht mit der Körpergröße des Tiers anwächst, sondern im Wesentlichen konstant ist. Gleiches gilt für den Durchmesser der feinsten Kapillaren: gerade so groß, dass ein rotes Blutkörperchen noch mit Mühe hindurchpasst.

In einer weiteren Veröffentlichung bringen West, Brown und Enquist einen zusätzlichen Gedanken in die Diskussion, um ihre These zu unterstützen. Für ein Tier ist es günstig, wenn es eine möglichst große Stoffwechselrate – die sich ihrerseits in vorteilhaften Eigenschaften wie Geschwindigkeit, Wehrhaftigkeit und Durchhaltevermögen äußert – mit möglichst geringem Aufwand erreichen kann. Man darf davon ausgehen, dass die Evolution dieses Optimierungsproblem im Verlauf der Jahrmillionen gelöst hat. Dies als Bedingung in diverse Gleichungen eingesetzt, ergibt abermals einen allometrischen Exponenten von 3/4.

Man ist ja geneigt, eine mathematische Modellierung schon deshalb zu akzeptieren, weil das Richtige herauskommt. Aber richtig begeistern konnte sie offensichtlich nicht, vor allem, weil ein unmittelbar einleuchtendes Prinzip hinter der Modellierung nicht so recht sichtbar war. Etliche Fachkollegen haben sich intensiv in Fachaufsätzen und Gegenreden mit West, Brown und Enquist beharkt. Dabei geht es, für einen Mathematiker wie mich ungewohnt, nicht in erster Linie darum, wer unter den zahlreichen Beteiligten richtig gerechnet hat – das ließe sich, vielleicht mit Mühe, aber doch irgendwann eindeutig entscheiden –, sondern ob das, was West und Kollegen in die Berechnungen einbezogen haben, das Wesentliche und das, was sie vernachlässigt haben, wirklich unwesentlich ist.

Am Ende hilft da nur der Blick in die empirischen Tatsachen. Aber o weh!, die sind noch verwirrender. Tom Kolokotrones und Kollegen haben 2010 Kleibers Diagramm sozusagen neu gezeichnet, diesmal aber mit einer viel größeren Datenbasis: K. B. McNab hatte den Grundumsatz von 637 Säugetierarten vermessen, deren Körpermasse immerhin sechs Zehnerpotenzen überspannte. Und wo Kleiber noch eine einigermaßen überzeugende Gerade in das doppeltlogarithmische Diagramm legen konnte, sieht das bei Kolokotrones eigentlich nur sehr wolkig aus.

Von einer streng gesetzmäßigen Beziehung ist da (in Fig. 1 des Artikels von Kolokotrones und Kollegen) nicht viel zu sehen. Aber selbstverständlich kann man trotzdem die Gerade berechnen, die die Datenpunkte am besten annähert; das ist die Lösung eines ziemlich einfachen Gleichungssystems (rote Linie im Diagramm). Und deren Steigung wäre der allometrische Exponent? Und wir wüssten jetzt endlich, ob 2/3 oder 3/4 der richtige Wert ist?

Pech gehabt. Was herauskommt, sind Werte wie 0,70 oder 0,71, also ziemlich genau die Mitte zwischen 2/3 = 0,666… und 3/4 = 0,75. Und die ganz schweren Tiere wollen überhaupt nicht passen, weswegen Kolokotrones und Kollegen sie nicht in die Berechnung einbezogen haben.

Na ja – vielleicht ist es ja gar keine Gerade, sondern eine Kurve. Nehmen wir die einfachste Kurve, die der mathematische Werkzeugkasten bereitstellt, eine quadratische Parabel, wieder so zurechtgemacht, dass sie optimal passt (blaue Kurve). Das sieht schon besser aus, irgendwie, vor allem bei den großen Tieren, aber nicht wie der wirklich große Durchbruch. Und eine biologische Rechtfertigung für den quadratischen Term will einem auch nicht einfallen.

Aber die Körpertemperatur zu berücksichtigen: Das bringt etwas. Der Grundgedanke ist: Je höher die Temperatur, desto schneller laufen die meisten chemischen Reaktionen ab und desto höher ist die Stoffwechselrate, die ein Tier bei ansonsten gleicher „Hardware“ – sprich Masse und Blutkreislauf – erzielen kann. Wenn man das in die Gleichungen einbaut, sinkt der „Fehlerterm“ (so die übliche Sprechweise, als ob alles, was das Modell nicht erklären kann, ein Messfehler wäre) drastisch ab. Dabei bleiben die biologischen Fragen offen: Wenn eine hohe Körpertemperatur so günstig ist, wieso sind nicht alle Säuger so heiß wie die heißesten?

Na gut. Welchen Erkenntnisgewinn kann man nun aus alledem ziehen? Das Ergebnis ist eher ernüchternd. Es gibt dieses Phänomen namens Allometrie, das wird durch einen Exponenten irgendwo zwischen 2/3 und 3/4 beschrieben, zumindest wenn man nicht so genau hinschaut. Und wenn man genauer hinschaut, kommt nichts weiter heraus als die banale Feststellung, dass das Leben kompliziert ist.

Bloß weil eine Gleichung eine eindeutige Lösung hat, muss das mathematische Modell, das durch die Gleichung ausgedrückt wird, noch nicht brauchbar sein. Immerhin reicht unsere Kenntnis von der Allometrie, so unvollständig sie ist, aus, einen Elefanten nicht aus Versehen mit LSD umzubringen. Und gelegentlich sind gerade die Abweichungen von der allgemeinen Regel interessant.

Das betrifft sogar mich persönlich. Zu den Größen, die unter die Gesetze der Allometrie fallen, zählt auch die Lebensspanne. Große Tiere leben tendenziell länger als kleine; was langsamer lebt, ist eben haltbarer. Für einen Säuger von Menschengröße kommen dabei größenordnungsmäßig 30 Jahre heraus. Ich bin durchaus erfreut darüber, dass der Mensch an dieser Stelle drastisch von der allgemeinen Regel abweicht; denn sonst wäre ich schon lange unter der Erde.

The post Von der Gefräßigkeit der Spitzmäuse und der Dauer des menschlichen Lebens originally appeared on the HLFF SciLogs blog.